
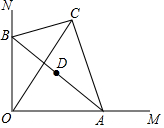
 如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:分析 ①先根据直角三角形30°的性质和勾股定理分别求AC和AB,由对称的性质可知:AB是OC的垂直平分线,所以OA=AC;
②当OC经过AB的中点E时,OC最大,则C、O两点距离的最大值为4;
③如图2,当∠ABO=30°时,易证四边形OACB是矩形,此时AB与CO互相平分,但所夹锐角为60°,明显不垂直,或者根据四点共圆可知:A、C、B、O四点共圆,则AB为直径,由垂径定理相关推论:平分弦(不是直径)的直径垂直于这条弦,但当这条弦也是直径时,即OC是直径时,AB与OC互相平分,但AB与OC不一定垂直;
④如图3,半径为2,圆心角为90°,根据弧长公式进行计算即可.
解答 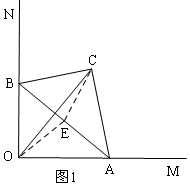 解:在Rt△ABC中,∵BC=2,∠BAC=30°,
解:在Rt△ABC中,∵BC=2,∠BAC=30°,
∴AB=4,AC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
①若C、O两点关于AB对称,如图1,
∴AB是OC的垂直平分线,
则OA=AC=2$\sqrt{3}$;
所以①正确;
②如图1,取AB的中点为E,连接OE、CE,
∵∠AOB=∠ACB=90°,
∴OE=CE=$\frac{1}{2}$AB=2,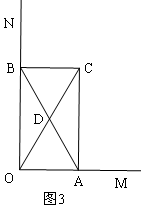
当OC经过点E时,OC最大,
则C、O两点距离的最大值为4;
所以②正确;
③如图2,当∠ABO=30°时,∠OBC=∠AOB=∠ACB=90°,
∴四边形AOBC是矩形,
∴AB与OC互相平分,
但AB与OC的夹角为60°、120°,不垂直,
所以③不正确;
④如图3,斜边AB的中点D运动路径是:以O为圆心,以2为半径的圆周的$\frac{1}{4}$,
则:$\frac{90π×2}{180}$=π,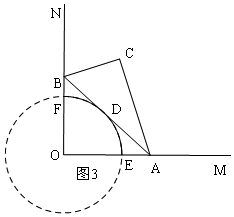
所以④不正确;
综上所述,本题正确的有:①②;
故答案为:①②.
点评 本题是三角形的综合题,考查了直角三角形30°的性质、直角三角形斜边中线的性质、等腰三角形的性质、轴对称的性质、线段垂直平分线的性质、动点运动路径问题、弧长公式,熟练掌握直角三角形斜边中线等于斜边一半是本题的关键,难度适中.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )
如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )| A. | 4+4-$\sqrt{4}$=6 | B. | 4+40+40=6 | C. | 4+$\root{3}{4+4}$=6 | D. | 4-1÷$\sqrt{4}$+4=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 用户每月用水量(m3) | 32及其以下 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43及其以上 |
| 户数(户) | 200 | 160 | 180 | 220 | 240 | 210 | 190 | 100 | 170 | 120 | 100 | 110 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
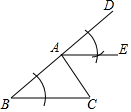 如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( )
如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( )| A. | ∠DAE=∠B | B. | ∠EAC=∠C | C. | AE∥BC | D. | ∠DAE=∠EAC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的角是对顶角 | |
| B. | 和为180°的两个角是邻补角 | |
| C. | 两条直线被第三条直线所截,同位角相等 | |
| D. | 过直线外一点,有且只有一条直线与已知直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
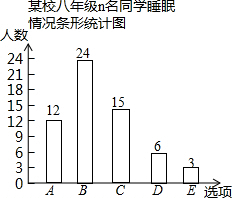 某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A,B,C,D,E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A,B,C,D,E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com