
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
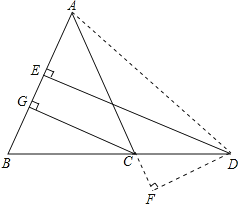
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

【答案】(1)当点D在BC的中点时,DE=DF,理由见解析;(2)DE+DF=CG.理由见解析;(3)当点D在BC延长线上时,(2)中的结论不成立,但有DE﹣DF=CG.理由见解析.
【解析】分析:(1)当点D在BC的中点时,DE=DF,根据AAS证△BED≌△CFD,根据全等三角形的性质推出即可;
(2)连接AD,根据三角形ABC的面积=三角形ABD的面积+三角形ACD的面积,进行分析证明;
(3)类似(2)的思路,仍然用计算面积的方法来确定线段之间的关系.即三角形ABC的面积=三角形ABD的面积-三角形ACD的面积.
详解:(1)当点D在BC的中点时,DE=DF,理由如下:
∵D为BC中点,∴BD=CD,
∵AB=AC,∴∠B=∠C,
∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°,
在△BED和△CFD中
∠B=∠C,∠DEB=∠DFC,BD=CD,
∴△BED≌△CFD(AAS),∴DE=DF.
(2)DE+DF=CG.
理由:连接AD,
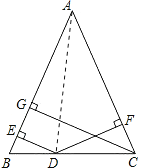
则S△ABC=S△ABD+S△ACD,即![]() ABCG=
ABCG=![]() ABDE+
ABDE+![]() ACDF,
ACDF,
∵AB=AC,∴CG=DE+DF.
(3)当点D在BC延长线上时,(2)中的结论不成立,但有DE﹣DF=CG.
理由:连接AD,则S△ABD=S△ABC+S△ACD,即![]() ABDE=
ABDE=![]() ABCG+
ABCG+![]() ACDF
ACDF
∵AB=AC,∴DE=CG+DF,即DE﹣DF=CG.
同理当D点在CB的延长线上时,(2)中结论不成立,则有DE﹣DF=CG,说明方法同上.


科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k﹣3)x+k2+1=0有两个不相等的实数根x1、x2 .
(1)求k的取值范围;
(2)试说明x1<0,x2<0;
(3)若抛物线y=x2﹣(2k﹣3)x+k2+1与x轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OAOB﹣3,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆直径,D、E为圆周上两点,且AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有( ) 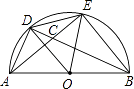
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=m2
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,![]() 可以理解为
可以理解为![]() ,它表示:数轴上表示数a的点到原点的距离,这是绝对值的几何意义。进一步地,数轴上的两个点A,B分别用数
,它表示:数轴上表示数a的点到原点的距离,这是绝对值的几何意义。进一步地,数轴上的两个点A,B分别用数![]() 表示,那么A,B两点之间的距离为
表示,那么A,B两点之间的距离为![]() ,反过来,式子
,反过来,式子![]() 的几何意义是:数轴上表示数
的几何意义是:数轴上表示数![]() 的点和表示数
的点和表示数![]() 的点之间的距离。利用此结论,
的点之间的距离。利用此结论,![]() 的意义就是数轴上表示数
的意义就是数轴上表示数![]() 的点到表示-2和表示3的点的距离之和是5,若
的点到表示-2和表示3的点的距离之和是5,若![]() 是整数,则符合
是整数,则符合![]() 的
的![]() 的个数是( )
的个数是( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )
A.3﹣ ![]() 或1+
或1+ ![]()
B.3﹣ ![]() 或3+
或3+ ![]()
C.3+ ![]() 或1﹣
或1﹣ ![]()
D.1﹣ ![]() 或1+
或1+ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com