
【题目】将正整数1,2,3,4,5,……排列成如图所示的数阵:
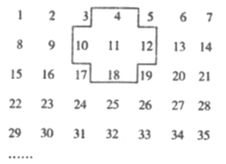
(1)十字框中五个数的和与框正中心的数11有什么关系?
(2)若将十字框上下、左右平移,可框住另外五个数,这五个数的和与框正中心的数还有这种规律吗?请说明理由;
(3)十字框中五个数的和能等于180吗?若能,请写出这五个数;若不能,请说明理由;
(4)十字框中五个数的和能等于2020吗?若能,请写出这五个数;若不能,请说明理由.
【答案】(1)十字框中五个数的和是正中心数的5倍;(2)十字框中五个数的和是正中心数的5倍,理由见解析;(3)不能,理由见解析;(4)这五个数是404,403,405,397,411.
【解析】
(1)把框住的数相加即可求解;
(2)设中心的数为![]() ,则其余4个数分别为
,则其余4个数分别为![]() ,
,![]() ,
,![]() ,
,![]() ,相加即可得到规律;
,相加即可得到规律;
(3)由(2)得五个数的和为5a,令5a=180,根据解得情况即可求解;
(4)由(2)得五个数的和为5a,令5a=2020,根据解得情况即可求解;

![]()
解:(1)十字框中五个数的和是正中心数的5倍.
∵十字框中五个数的和![]() ,
,
∴十字框中五个数的和是正中心数的5倍.
(2)五个数的和与框正中心的数还有这种规律.
设中心的数为![]() ,则其余4个数分别为
,则其余4个数分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
∴十字框中五个数的和是正中心数的5倍.
(3)十字框中五个数的和不能等于180.
∵当![]() 时,解得
时,解得![]() ,
,
![]() ,36在数阵中位于第6排的第1个数,其前面无数字,
,36在数阵中位于第6排的第1个数,其前面无数字,
∴十字框中五个数的和不能等于180.
(4)十字框中五个数的和能等于2020.
∵当![]() 时,解得
时,解得![]() ,
,
![]() ,404在数阵中位于第58排的第5个数,
,404在数阵中位于第58排的第5个数,
∴十字框中五个数的和能等于2020,
这五个数是404,403,405,397,411.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】用若干等长的木棒按如图的方式摆放.

![]() 填写下表:
填写下表:
图形编号 |
|
|
|
|
|
|
木棒根数 | 7 | 12 | ______ | ______ | ______ |
|
![]() 搭第n个图形需要多少根木棒?
搭第n个图形需要多少根木棒?
![]() 搭第几个图形需要2017根木棒?
搭第几个图形需要2017根木棒?
查看答案和解析>>
科目:初中数学 来源: 题型:
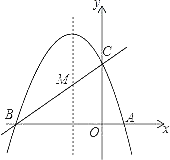
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
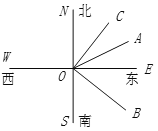
【题目】如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东56°,射线 OC在∠NOE内,且∠NOC与∠BOS互余,射线OA平分∠BON,图中与∠COA互余的角是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的分式方程![]() 的解为正数,且使关于y的不等式组
的解为正数,且使关于y的不等式组 的解集为y<﹣2,则符合条件的所有整数a的和为( )
的解集为y<﹣2,则符合条件的所有整数a的和为( )
A. 10B. 12C. 14D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别从
,甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向而行.已知甲车速度为
两地同时出发,相向而行.已知甲车速度为![]() ,乙车速度为
,乙车速度为![]() ,经过
,经过![]() 后两车相距
后两车相距![]() ,则
,则![]() 的值是( )
的值是( )
A.2B.10C.2或10D.2或2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:![]() (p,q是正整数,且
(p,q是正整数,且![]() ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:![]() .
.
例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=![]() .
.
(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为![]() ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
(3)在(2)所得“和谐数”中,求F(t)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com