
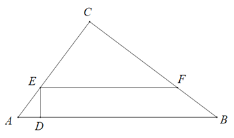
【题目】如图,在直角△ABC中,∠C=90°,AC=15,BC=20,点D为AB边上一动点,若AD的长度为m,且m的范围为0<m<9,在AC与BC边上分别取两点E、F,满足ED⊥AB,FE⊥ED.
(1)求DE的长度;(用含m的代数式表示)
(2)求EF的长度;(用含m的代数式表示)
(3)请根据m的不同取值,探索过D、E、F三点的圆与△ABC三边交点的个数.
【答案】(1)![]() ;(2) 25-
;(2) 25-![]() ; (3)见解析.
; (3)见解析.
【解析】
(1)先证△ADE∽△ACB,得到![]() =
=![]() ,代入即可得到DE=
,代入即可得到DE=![]() ;
;
(2)由勾股定理得到AE=![]() ,利用两个角相等的两个三角形相似得到△ADE∽△ECF,利用相似三角形对应边成比例,得到
,利用两个角相等的两个三角形相似得到△ADE∽△ECF,利用相似三角形对应边成比例,得到![]() =
=![]() ,代入即可得到EF=25-
,代入即可得到EF=25-![]() ;
;
(3)先分别求出过D、E、F三点的⊙O与AC和BC相切时m=![]() 和m=
和m=![]() ,再分0<m<
,再分0<m<![]() ,m=
,m=![]() ,
,![]() <m<
<m<![]() ,m=
,m=![]() ,
,![]() <m<9,五种情况进行说明.
<m<9,五种情况进行说明.
解:(1)∵ED⊥AB,∴∠EDA=90°,∴∠EDA=∠C=90°,
∵∠A=∠A,∴△ADE∽△ACB,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
∴DE=![]() ;
;
(2)在RT△ADE中,
AE=![]() =
=![]() ,
,
∵ED⊥AB,FE⊥ED
∴∠EDA=∠DEF=90°,
∴EF∥AB,
∴∠A=∠CEF,
又∵∠EDA=∠C,
∴△ADE∽△ECF,
∴![]() =
=![]() ,∴m:(15-
,∴m:(15-![]() )=
)=![]() :EF,
:EF,
∴EF=25-![]() .
.
(3)当ED:EF=3:4,⊙O与AC相切于点E,
![]() :(25-
:(25-![]() )=3:4,m=
)=3:4,m=![]() ,
,
当ED:EF=4:3,⊙O与BC相切于点F,
![]() :(25-
:(25-![]() )=4:3,m=
)=4:3,m=![]() ,
,
情况一:当0<m<![]() 时,⊙O与△ABC有六个交点;
时,⊙O与△ABC有六个交点;
情况二:当m=![]() 时,⊙O与△ABC有五个交点;
时,⊙O与△ABC有五个交点;
情况三:当![]() <m<
<m<![]() 时,⊙O与△ABC有六个交点;
时,⊙O与△ABC有六个交点;
情况四:当m=![]() 时,⊙O与△ABC有五个交点;
时,⊙O与△ABC有五个交点;
情况五:当![]() <m<9时,⊙O与△ABC有六个交点.
<m<9时,⊙O与△ABC有六个交点.
故答案为:(1)![]() ;(2) 25-
;(2) 25-![]() ; (3)见解析.
; (3)见解析.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
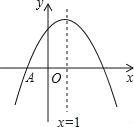
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
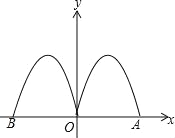
【题目】如图,抛物线y=﹣2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
A. 0<m<![]() B.
B. ![]() <m<
<m<![]()
C. 0<m<![]() D. m<
D. m<![]() 或m<
或m<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
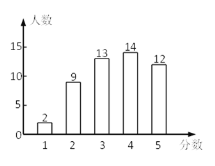
【题目】光明中学全体学生1100人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
(1)填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩(单位:分) |
(2)估计光明中学全体学生社会实践活动成绩的总分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2=![]() 的图象交于点A(﹣1,3)、B(n,﹣1).
的图象交于点A(﹣1,3)、B(n,﹣1).
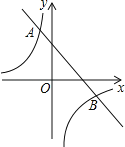
(1)求反比例函数的解析式;
(2)当y1>y2时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
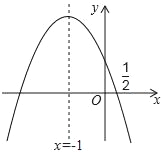
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,且OA、OB分别与反比例函数y=![]() (x>0)、y=﹣
(x>0)、y=﹣![]() (x<0)的图象交于A、B两点,则tan∠OAB的值是( )
(x<0)的图象交于A、B两点,则tan∠OAB的值是( )

A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com