
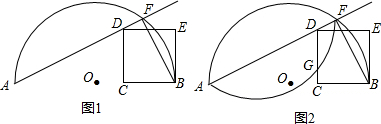
如图1,⊙O的直径CD=4,AD⊥DC,BC⊥DC,AD=2,BC=6,P是⊙O上的一个动点.
(1)求证OA⊥AB;
(2)若△APB的面积记为S,求S的最大值与最小值,并分别指出此时P点所在的位置;
 (3)若以P为圆心,BP长为半径作圆,是否存在⊙P与⊙O相切?请说明理由.
(3)若以P为圆心,BP长为半径作圆,是否存在⊙P与⊙O相切?请说明理由.

证明:(1)过A点作AE⊥BC于E, 1分
∵AD⊥DC,BC⊥DC∴ 四边形ADCE为矩形 1分
∴ EC=AD=2 ∴BE=6-2=4 AE=DC=4
∴△ABE为等腰直角三角形∴∠B=45° 1分
∵△ADO为等腰直角三角形 ∴∠AOD=45°
∴∠AOC=135° ,根据四边形内角和为360°∴∠OAC=90° ∴OA⊥AB 1分
(2) 设AO及延长线交圆于P1、 P2点,过P1作P1F∥AB交BC于F点,
∵OA⊥AB ∴P1到AB的距离最短,P2到AB的距离最长 2分
∵ △ADO为等腰直角三角形 ∴AO=![]() 2
2![]()
![]() AP1=2
AP1=2![]() -2,AP2=2
-2,AP2=2![]() +2 2分
+2 2分
由(1)可得AB=4![]() ,所以S的最小值为8+4
,所以S的最小值为8+4![]() ,最大值为8-4
,最大值为8-4![]() 2分
2分
(3)不存在⊙P与⊙O相切 1分
∵ BO=![]() ,则BP的最大值为=
,则BP的最大值为=![]() +2,最小值为=
+2,最小值为=![]() -2,OP=2, 1分
-2,OP=2, 1分
∵P在圆上,所以两圆不可能外切 1分
∵两圆的半径之差的范围是![]() ,而d=2<
,而d=2<![]() ,
,
∴不存在相切的可能性![]()


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
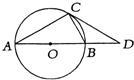 20、如图AB是⊙O的直径,AB=OD,BC=BD,请根据已知条件和所给图形,写出三个正确的结论:(不添加辅助线)①
20、如图AB是⊙O的直径,AB=OD,BC=BD,请根据已知条件和所给图形,写出三个正确的结论:(不添加辅助线)①查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
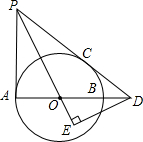 (2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
(2013•北京)如图AB是⊙O的直径,PA,PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.| 3 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com