
【题目】已知:![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,
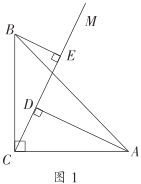
(1)如图1,①线段![]() 和
和![]() 的数量关系是__________;
的数量关系是__________;
②请写出线段![]() ,
,![]() ,
,![]() 之间的数量关系并证明.
之间的数量关系并证明.
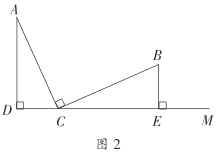
(2)如图2,若已知条件不变,上述结论②还成立吗?如果不成立,请直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)①![]() .②结论:
.②结论:![]() ,理由见解析;(2)
,理由见解析;(2)![]()
【解析】
(1)①结论:CD=BE;②结论:AD=BE+DE,只要证明△ACD≌△CBE,即可解决问题.
(2)结论不成立.结论:DE=AD+BE.证明方法类似(1).
(1)①![]() .
.
理由如下:
∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ACD和△CBE中,
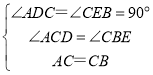 ,
,
∴△ACD≌△CBE,
∴CD=BE.
②结论:![]() .
.
理由如下:
由①得:△ACD≌△CBE,
![]() ,
,
![]() ,
,
![]() .
.
(2)②中的结论不成立.结论:DE=AD+BE.
理由如下:
∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠B=90°,
∴∠ACD=∠B,
在△ACD和△CBE中,
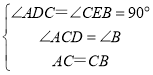 ,
,
∴△ACD≌△CBE,
∴AD=CE,CD=BE,
∵DE=CD+CE=BE+AD,
∴DE=AD+BE.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
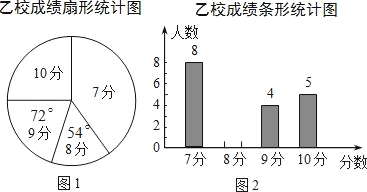
【题目】(10分)甲、乙两校参加市教育局举办的初中生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 |
| 8 |
(1)请将甲校成绩统计表和图2的统计图补充完整;
(2)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
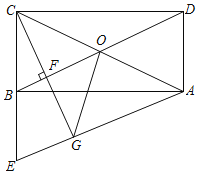
【题目】如图,在矩形ABCD中,AC、BD相交于点O,过点A作BD的平行线AE交CB的延长线于点E.
(1)求证:BE=BC;
(2)过点C作CF⊥BD于点F,并延长CF交AE于点G,连接OG.若BF=3,CF=6,求四边形BOGE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a+b=1,ab=﹣1,设S1=a+b,S2=a2+b2,S3=a3+b3,…,Sn=an+bn
(1)计算S2.
(2)请阅读下面计算S3的过程:
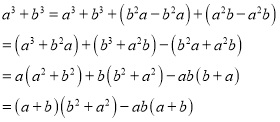
∵a+b=1,ab=﹣1
∴S3=a3+b3=(a+b)(a2+b2)﹣ab(a+b)=1×S2﹣(﹣1)=S2+1= .
你读懂了吗?请你先填空完成(2)中S3的计算结果,再用你学到的方法计算S4
(3)试写出Sn﹣2,Sn﹣1,Sn三者之间的数量关系式(不要求证明,且n是不小于2的自然数),根据得出的数量关系计算S7.
查看答案和解析>>
科目:初中数学 来源: 题型:
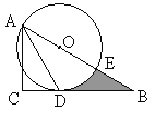
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧![]() 所围成的阴影部分的面积(结果保留根号和
所围成的阴影部分的面积(结果保留根号和![]() )。
)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
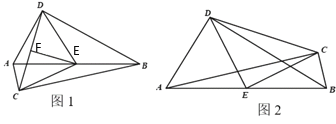
【题目】已知:如图,Rt△ABC和Rt△ABD中,∠ACB=∠ADB=90°,E为AB中点.
(1)若两个直角三角形的直角顶点在AB的异侧(如图1),连接CD,取CD中点F,连接EF、DE、CE,则DE与CE数量关系为 ,EF与CD位置关系为 ;
(2)若两个直角三角形的直角顶点在AB的同侧(如图2),连接CD、DE、CE.
①若∠CAB=25°,∠DBA=35°,判断△DEC的形状,并说明理由;
②若∠CAB+∠DBA=![]() ,当
,当![]() 为多少度时,△DEC为等腰直角三角形,并说明理由.
为多少度时,△DEC为等腰直角三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
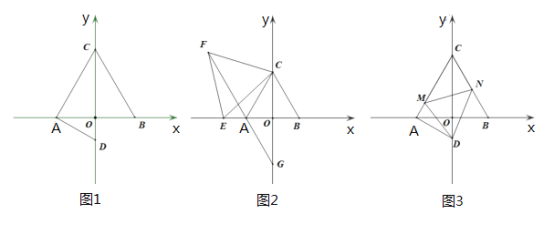
【题目】如图,等边![]() 中,
中,![]() ,
,![]() 关于
关于![]() 轴对称,
轴对称,![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,
,![]() .
.
(1)如图1,求![]() 点坐标;
点坐标;
(2)如图2,![]() 为
为![]() 轴负半轴上任一点,以
轴负半轴上任一点,以![]() 为边作等边
为边作等边![]() ,
,![]() 的延长线交
的延长线交![]() 轴于点
轴于点![]() ,求
,求![]() 的长;
的长;
(3)如图3,在(1)的条件下,以![]() 为顶点作
为顶点作![]() 的角,它的两边分别与
的角,它的两边分别与![]() 、
、![]() 交于点
交于点![]() 和
和![]() ,连接
,连接![]() .探究线段
.探究线段![]() 、
、![]() 、
、![]() 之间的关系,并子以证明.
之间的关系,并子以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com