
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)写出数轴上点A表示的数;
(2)将长方形OABC沿数轴向右水平移动,移动后的长方形记为![]() ,若移动后的长方形
,若移动后的长方形![]() 与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的
与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的![]() 时,写出数轴上点
时,写出数轴上点![]() 表示的数;
表示的数;

 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论: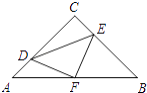
①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形,
③DE长度的最小值为4;
④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
A.①②③
B.①④⑤
C.①③④
D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有330名男生,为了解该年级男生1000米跑步成绩(单位:分/秒)的情况,从中随机抽取30名男生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a.1000米跑步的频数分布表如下:
分组 | 3′17″<x≤3′ 37″ | 3′37″<x≤3′ 57″ | 3′ 57″<x≤4′ 17″ | 4′ 17″<x≤4′ 37″ | 4′ 37″<x≤4′ 57″ | 4′ 57″<x≤5′ 17″ |
频数 | 10 | 9 | m | 2 | 2 | 1 |
注:3′37″即3分37秒
b.1000米跑步在3′37″<x≤3′57″这一组是:
3′39 ″ 3′42 ″ 3′45 ″ 3′45″ 3′50 ″ 3′52 ″ 3′53″ 3′55″ 3′57″
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)根据表频数分布表画出相应的频数分布直方图.
(3)若男生1000米跑步成绩等于或者优于3′52″,成绩记为优秀.请估计全年级男生跑步成绩达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①CF=2AF;②tan∠CAD=![]() ;
;
③DF=DC;④△AEF∽△CAB;⑤ S四边形CDEF=![]() S△ABF ,其中正确的结论有( )
S△ABF ,其中正确的结论有( )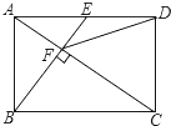
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了![]() 层,将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层,将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]()
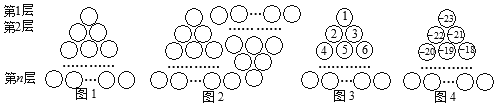
如果图中的圆圈共有13层,请解决下列问题:
(1)若自上往下,在图①每个圆圈中填上一串连续的正整数1,2,3,4,…,得到图3,写出第11层最左边这个圆圈中的数;
(2)若自上往下,在图①每个圆圈中填上一串连续的整数-23,-22,-21,20,…,得到图4,写出第10层最右边圆圈内的数;
(3)根据以上规律,求图4中第1层到第10层所有圆圈中各数之和(写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知α是锐角,且点A( ![]() ,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函数y=﹣x2+x+3的图象上,那么a、b、c的大小关系是( )
,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函数y=﹣x2+x+3的图象上,那么a、b、c的大小关系是( )
A.a<b<c
B.a<c<b
C.b<c<a
D.c<b<a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图)
小淇同学作法如下:
(1)在直线l上任意取一点C,连接AC;
(2)作AC的中点O;
(3)以O为圆心,OA长为半径画弧交直线l于点B,如图所示;
(4)作直线AB.
则直线AB就是所要作图形.
你认为小淇的作法正确吗?如果不正确,请画出一个反例;如果正确,请给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90,AC=BC,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.
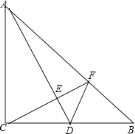
查看答案和解析>>
科目:初中数学 来源: 题型:
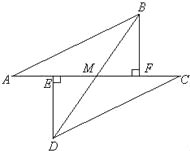
【题目】如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com