
【题目】王浩同学用木板制作一个带有卡槽的三角形手机架,如图所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2).

【答案】王浩同学能将手机放入卡槽AB内,理由详见解析.
【解析】试题分析:
由题意可知,手机能不能放入卡槽AB内可以通过线段AB的长与手机的长17cm的比较来判断. 因此,本题就转化为如何求解线段AB的长. 分析已知条件可知,通过作△ABC的边BC上的高AD,可以利用已知条件中∠ACB的度数与边AC的长求解Rt△ADC,进而通过勾股定理得到线段AB的长.
试题解析:
王浩同学能将手机放入卡槽AB内. 理由如下.
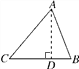
如图,过点A作AD⊥BC,垂足为D.
∵∠ACB=50°,AC=20cm,
∴在Rt△ADC中,
![]() (cm),
(cm),
![]() (cm),
(cm),
∵BC=18cm,
∴BD=BC-CD≈18-12=6(cm),
∴在Rt△ADB中,![]() (cm).
(cm).
∵![]() ,
,![]() ,
,
又∵![]() ,
,
∴AB>17,即卡槽AB的长度大于手机的长,
∴王浩同学能将手机放入卡槽AB内.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,![]() =_____.
=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.

(1)求证:FD是⊙O的切线;
(2)若AF=8,tan∠BDF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q.
(1)当点P运动到Q、C两点重合时(如图①),求AP的长;
(2)点P运动过程中,有几个位置(几种情况)使△CQD的面积为![]() (直接写出答案)?
(直接写出答案)?
(3)当使△CQD的面积为![]() ,且Q位于以CD为直径的半圆上,CQ>QD时(如图②),求AP的长.
,且Q位于以CD为直径的半圆上,CQ>QD时(如图②),求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年2月份,某市经济开发区完成出口316000000美元,将这个数据316000000用科学记数法表示应为( )
A.316×106
B.31.6×107
C.3.16×108
D.0.316×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 AD 是△ABC 的一条高,∠BAD=70°,∠CAD=20°,则∠BAC 的度数为( )
A. 50° B. 60° C. 90° D. 50°或 90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com