
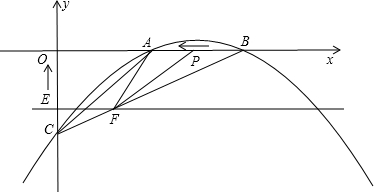
如图,已知抛物线 交x轴的正半轴于点A,交y轴于点B.
交x轴的正半轴于点A,交y轴于点B.
【小题1】求直线AB的解析式;
【小题2】设P(x,y)(x>0)是直线y = x上的一点,Q是OP 的中点(O是原点),以PQ为对角线作正方形PEQF,若正方形PEQF与直线AB有公共点,求x的取值范围;
【小题3】在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值.
【小题1】对于 ,令x=0,得y=4,即B(0,4);…
,令x=0,得y=4,即B(0,4);…
令y=0,即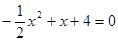 ,解得:x1 = —2,x2 = 4,即A(4,0)
,解得:x1 = —2,x2 = 4,即A(4,0)
设直线AB的解析式为y =" kx" + b,
把A(4,0),B(0,4)分别代入上式,得 ,解得:k = —1,b = 4,
,解得:k = —1,b = 4,
∴直线AB的解析式为y = —x + 4。
【小题1】当点P(x,y)在直线AB上时,由x = —x + 4,得:x = 2,
当点Q在直线AB上时,依题意可知Q( ,
, ),由
),由 ,得:x = 4,
,得:x = 4,
∴若正方形PEQF与直线AB有公共点,则x的取值范围为2≤x≤4;
【小题1】当点E(x, )在直线AB上时,
)在直线AB上时,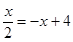 ,解得
,解得 ,
,
①当 时,直线AB分别与PE、PF交于点C、D,此时PC = x—(—x+4) = 2x—4,
时,直线AB分别与PE、PF交于点C、D,此时PC = x—(—x+4) = 2x—4,
∵ PD = PC,
∴ S△PCD =
∴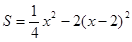

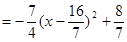
∵ ,
,
∴当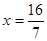 时,
时,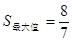
②当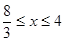 时,直线AB分别与QE、QF交于点M、N,此时,
时,直线AB分别与QE、QF交于点M、N,此时,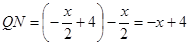
∵ QM = QN,
∴ S△QMN=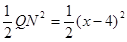
即 ,
,
其中,当 时,
时,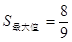
综合①、②,当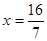 时,
时,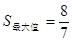
解析【小题1】抛物线的解析式中,令x=0可求出B点的坐标,令y=0可求出A点的坐标,然后用待定系数法即可求出直线AB的解析式;
【小题1】可分别求出当点P、点Q在直线AB上时x的值,即可得到所求的x的取值范围;
【小题1】此题首先要计算出一个关键点:即直线AB过E、F时x的值(由于直线AB与直线OP垂直,所以直线AB同时经过E、F),此时点E的坐标为(x, ),代入直线AB的解析式即可得到x=
),代入直线AB的解析式即可得到x=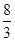 ;
;
①当2≤x<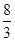 时,直线AB与PE、PF相交,设交点为C、D;那么重合部分的面积为正方形QEPF和等腰Rt△PDC的面积差,由此可得到关于S、x的函数关系式,进而可根据函数的性质及自变量的取值范围求出S的最大值及对应的x的值;
时,直线AB与PE、PF相交,设交点为C、D;那么重合部分的面积为正方形QEPF和等腰Rt△PDC的面积差,由此可得到关于S、x的函数关系式,进而可根据函数的性质及自变量的取值范围求出S的最大值及对应的x的值;
②当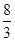 ≤x≤4时,直线AB与QE、QF相交,设交点为M、N;此时重合部分的面积为等腰Rt△QMN的面积,可参照①的方法求出此时S的最大值及对应的x的值;
≤x≤4时,直线AB与QE、QF相交,设交点为M、N;此时重合部分的面积为等腰Rt△QMN的面积,可参照①的方法求出此时S的最大值及对应的x的值;
综合上述两种情况,即可比较得出S的最大值及对应的x的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
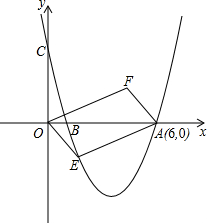 AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.
AB=5OB,设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
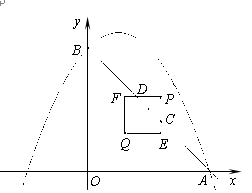
如图,已知抛物线![]() 交x轴于C(x1,0),D(x2,0)两点,(x1<x2)且
交x轴于C(x1,0),D(x2,0)两点,(x1<x2)且![]()
(1)试确定m的值;
(2)过点A(-1,-5)和抛物线的顶点M的直线交x轴于点B,求B点的坐标;
(3)设点P(a,b)是抛物线上点C到点M之间的一个动点(含C、M点),![]() 是以PO为腰、底边OQ在x轴上的等腰三角形,过点Q作x轴的垂线交直线AM于点R,连结PR。设
是以PO为腰、底边OQ在x轴上的等腰三角形,过点Q作x轴的垂线交直线AM于点R,连结PR。设![]() 的面积为S,求S与a之间的函数关系式。
的面积为S,求S与a之间的函数关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线![]() 交x轴的正半轴于点A,交y轴于点B.
交x轴的正半轴于点A,交y轴于点B.
1.求A、B两点的坐标,并求直线AB的解析式;
2.设![]() (
(![]() )是直线
)是直线![]() 上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF.若正方形PEQF与直线AB有公共点,求x的取值范围;
上的一点,Q是OP的中点(O是原点),以PQ为对角线作正方形PEQF.若正方形PEQF与直线AB有公共点,求x的取值范围;
3.在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广东省初三第二学期质量检查数学试卷(解析版) 题型:解答题
如图,已知抛物线 交x轴的正半轴于点A,交y轴于点B.
交x轴的正半轴于点A,交y轴于点B.
1.求直线AB的解析式;
2.设P(x,y)(x>0)是直线y = x上的一点,Q是OP 的中点(O是原点),以PQ为对角线作正方形PEQF,若正方形PEQF与直线AB有公共点,求x的取值范围;
3.在(2)的条件下,记正方形PEQF与△OAB公共部分的面积为S,求S关于x的函数解析式,并探究S的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com