解:(1)把点A(1,3)代入反比例解析式中得:k=3,
∴反比例解析式为y=

,
又把点B(n,-1)代入反比例解析式中得:n=-3,
即点B(-3,-1),A(1,3),又一次函数y=mx+b,
∴将A和B代入一次函数得:

,解得

,
∴一次函数解析式为y=x+2;
(2)由y=x+2,令y=0,解得x=-2,则|OC|=2,点A的纵坐标为3,
故△AC0的面积S=

|OC|•3=3;
(3)P(3,1)或P(-3,-1).
分析:(1)把点A的坐标代入反比例解析式中求出k的值,确定出反比例的解析式,然后把B的坐标代入反比例解析式中求出n的值确定出点B的坐标,把A和B的坐标代入一次函数解析式中得到关于m和b的二元一次方程组,求出方程组的解得到m与b的值,确定出一次函数的解析式;
(2)令一次函数解析式中y=0求出点C的坐标,进而得到|OC|的长度即为三角形OCA的底,高为点A的纵坐标,利用三角形的面积公式即可求出△AC0的面积;
(3)由题意可知,找出点A关于y=x的对称点P
1,且找出P关于原点的对称点P
2,能使得点A,O,P构成等腰三角形.根据对称的特点写出P
1和P
2的坐标即可.
点评:此题考查学生掌握确定函数解析式的方法:反比例需要一个点坐标确定,一次函数需要两点坐标确定;掌握等腰三角形的判断方法以及有关对称点的特点,是一道中档题.

 的图象与一次函散y=mx+b的图象交于两点A(1,3),B(n,-1).一
的图象与一次函散y=mx+b的图象交于两点A(1,3),B(n,-1).一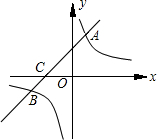 次函数y=mx+b的图象与x轴交于点C.
次函数y=mx+b的图象与x轴交于点C. ,
, ,解得
,解得 ,
, |OC|•3=3;
|OC|•3=3;

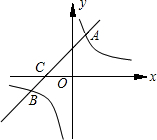 次函数y=mx+b的图象与x轴交于点C.
次函数y=mx+b的图象与x轴交于点C.