
分析 (1)首先利用整式的乘法计算方法计算,进一步合并求证得出答案即可;
(2)把y=x+1代入(1)中,整理利用二次函数的性质解决问题.
解答 解:(1)证明:
z=3x(3y-x)-(4x-3y)(x+3y)
=9xy-3x2-(4x2+9xy-9y2)
=9xy-3x2-4x2-9xy+9y2
=-7x2+9y2
∵x是3的倍数时,
∴z能被9整除.
(2)当y=x+1时,
则z=-7x2+9(x+1)2
=2x2+18x+9
=2(x+$\frac{9}{2}$)2-$\frac{63}{2}$
∵2(x+$\frac{9}{8}$)2≥0
∴z的最小值是-$\frac{63}{2}$.
点评 此题考查二次函数的性质,整式的混合运算,利用整式的计算方法先化简是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 0.18×107 | B. | 1.8×106 | C. | 1.8×107 | D. | 18×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
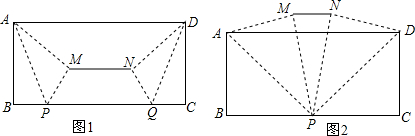
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.
超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com