
【题目】如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论:
①∠AFC=120°;
②△AEF是等边三角形;
③AC=3OG;
④S△AOG=![]() S△ABC
S△ABC
其中正确的是______.(把所有正确结论的序号都选上)
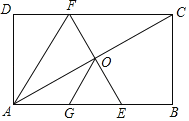
【答案】①②④.
【解析】试题分析:根据直角三角形斜边上的中线等于斜边的一半可得OG=AG=GE=![]() AE,再根据等边对等角可得∠OAG=30°,∠EOG=60°,从而根据矩形的性质得到∠ACF=30°,因此由线段垂直平分线的性质可得FC=AF,因此可根据等边对等角得到∠FAE=30°,根据三角形的内角和求得∠AFC=120°,故①正确;
AE,再根据等边对等角可得∠OAG=30°,∠EOG=60°,从而根据矩形的性质得到∠ACF=30°,因此由线段垂直平分线的性质可得FC=AF,因此可根据等边对等角得到∠FAE=30°,根据三角形的内角和求得∠AFC=120°,故①正确;
由∠AFC=120°,∠FCA=30°,可知∠AFE=60°,因此△AEF是等边三角形,故②正确;
连接CE,则根据三角形的中位线可知CE=2OG,由矩形的性质可得四边形AECF是菱形,且![]() ,由OE=OG,OA=
,由OE=OG,OA=![]() AC,可知
AC,可知![]() ,解得AC=
,解得AC=![]() OG,故③不正确;
OG,故③不正确;
令AE=2a,则OG=OE=a,AO=![]() a,AC=2
a,AC=2![]() a,由S△AOE=
a,由S△AOE=![]() ×a×
×a×![]() a=
a=![]() 2,S矩形ABCD=3a×
2,S矩形ABCD=3a×![]() a=3
a=3![]() a2 ,即S△AOG=
a2 ,即S△AOG=![]() S△ABC,故④正确.
S△ABC,故④正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过B(﹣1,0),D(﹣2,5)两点,与x轴另一交点为A,点H是线段AB上一动点,过点H的直线PQ⊥x轴,分别交直线AD、抛物线于点Q,P.
经过B(﹣1,0),D(﹣2,5)两点,与x轴另一交点为A,点H是线段AB上一动点,过点H的直线PQ⊥x轴,分别交直线AD、抛物线于点Q,P.
(1)求抛物线的解析式;
(2)是否存在点P,使∠APB=90°,若存在,求出点P的横坐标,若不存在,说明理由;
(3)连接BQ,一动点M从点B出发,沿线段BQ以每秒1个单位的速度运动到Q,再沿线段QD以每秒![]() 个单位的速度运动到D后停止,当点Q的坐标是多少时,点M在整个运动过程中用时t最少?
个单位的速度运动到D后停止,当点Q的坐标是多少时,点M在整个运动过程中用时t最少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲从
两地,甲从![]() 地去
地去![]() 地,乙从
地,乙从![]() 地去
地去![]() 地然后立即原路返回
地然后立即原路返回![]() 地,返回时的速度是原来的2倍,如图是甲、乙两人离
地,返回时的速度是原来的2倍,如图是甲、乙两人离![]() 地的距离
地的距离![]() (千米)和时间
(千米)和时间![]() (小时)之间的函数图象.
(小时)之间的函数图象.
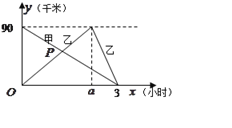
请根据图象回答下列问题:
(1)![]() 、
、![]() 两地的距离是 千米,
两地的距离是 千米, ![]() ;
;
(2)求![]() 的坐标,并解释它的实际意义;
的坐标,并解释它的实际意义;
(3)请直接写出当![]() 取何值时,甲乙两人相距15千米.
取何值时,甲乙两人相距15千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空: a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市今年参加中考的人数约为15000人,将15000用科学记数法表示为( )
A.0.15×105B.1.5×104C.15×103D.1.5×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共有19条运营线路,覆盖北京市11个辖区.据统计,2017 年地铁每小时客运量是2002年地铁每小时客运量的4倍,2017年客运240万人所用的时间比2002年客运240万人所用的时间少30小时,求2017年地铁每小时的客运量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值
(1)4x﹣x2+2x3﹣(3x2+x+2x3),其中x=3.
(2)4x2﹣xy﹣(![]() y2+2x2)+2(3xy﹣
y2+2x2)+2(3xy﹣![]() y2),其中x=5,y=
y2),其中x=5,y=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com