练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    设E、F是正方形ABCD的边BC、CD的中点，若AB=4，则△AEF的面积是（     ）。
    6
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

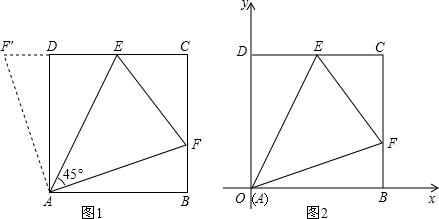
    （2012•惠山区一模）阅读与证明：
    如图，已知正方形ABCD中，E、F分别是CD、BC上的点，且∠EAF=45°，

    求证：BF+DE=EF．
    分析：证明一条线段等于另两条线段的和，常用“截长法”或“补短法”，将线段BF、DE放在同一直线上，构造出一条与BF+DE相等的线段．如图1延长ED至点F′，使DF′=BF，连接A F′，易证△ABF≌△ADF′，进一步证明△AEF≌△AEF′，即可得结论．
    （1）请你将下面的证明过程补充完整．
    证明：延长ED至F′，使DF′=BF，
    ∵四边形ABCD是正方形
    ∴AB=AD，∠ABF=∠ADF′=90°，
    ∴△ABF≌△ADF’（SAS）
    应用与拓展：如图建立平面直角坐标系，使顶点A与坐标原点O重合，边OB、OD分别在x轴、y轴的正半轴上．
    （2）设正方形边长OB为30，当E为CD中点时，试问F为BC的几等分点？并求此时F点的坐标；
    （3）设正方形边长OB为30，当EF最短时，直接写出直线EF的解析式：
    y=-x+30
    		2
    y=-x+30
    		2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    阅读与证明：
    如图，已知正方形ABCD中，E、F分别是CD、BC上的点，且∠EAF=45°，

    求证：BF+DE=EF．
    分析：证明一条线段等于另两条线段的和，常用“截长法”或“补短法”，将线段BF、DE放在同一直线上，构造出一条与BF+DE相等的线段．如图1延长ED至点F′，使DF′=BF，连接A F′，易证△ABF≌△ADF′，进一步证明△AEF≌△AEF′，即可得结论．
    （1）请你将下面的证明过程补充完整．
    证明：延长ED至F′，使DF′=BF，
    ∵四边形ABCD是正方形
    ∴AB=AD，∠ABF=∠ADF′=90°，
    ∴△ABF≌△ADF’（SAS）
    应用与拓展：如图建立平面直角坐标系，使顶点A与坐标原点O重合，边OB、OD分别在x轴、y轴的正半轴上．
    （2）设正方形边长OB为30，当E为CD中点时，试问F为BC的几等分点？并求此时F点的坐标；
    （3）设正方形边长OB为30，当EF最短时，直接写出直线EF的解析式：______．

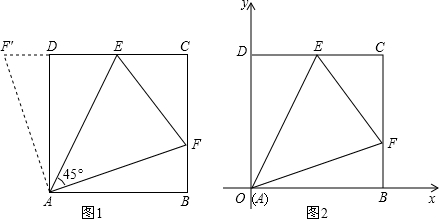
    查看答案和解析>>

    科目：初中数学 来源：2012年江苏省无锡市惠山区中考数学一模试卷（解析版） 题型：解答题

    阅读与证明：
    如图，已知正方形ABCD中，E、F分别是CD、BC上的点，且∠EAF=45°，

    求证：BF+DE=EF．
    分析：证明一条线段等于另两条线段的和，常用“截长法”或“补短法”，将线段BF、DE放在同一直线上，构造出一条与BF+DE相等的线段．如图1延长ED至点F′，使DF′=BF，连接A F′，易证△ABF≌△ADF′，进一步证明△AEF≌△AEF′，即可得结论．
    （1）请你将下面的证明过程补充完整．
    证明：延长ED至F′，使DF′=BF，
    ∵四边形ABCD是正方形
    ∴AB=AD，∠ABF=∠ADF′=90°，
    ∴△ABF≌△ADF’（SAS）
    应用与拓展：如图建立平面直角坐标系，使顶点A与坐标原点O重合，边OB、OD分别在x轴、y轴的正半轴上．
    （2）设正方形边长OB为30，当E为CD中点时，试问F为BC的几等分点？并求此时F点的坐标；
    （3）设正方形边长OB为30，当EF最短时，直接写出直线EF的解析式：______

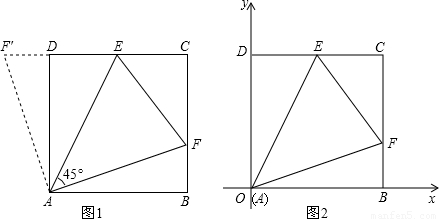
    查看答案和解析>>

    科目：初中数学 来源：江苏期中题 题型：解答题

    阅读与证明：    
    如图，已知正方形ABCD中，E、F分别是CD、BC上的点，且∠EAF＝45 °，
    求证：BF＋DE＝EF。
    分析：证明一条线段等于另两条线段的和，常用“截长法”或“补短法”，将线段BF、DE放在同一直线上，构造出一条与BF＋DE相等的线段。如图1延长ED至点F'，使DF'＝BF，连接A F'，易证△ABF≌△ADF'，进一步证明△AEF≌△AEF'，即可得结论。
    （1）请你将下面的证明过程补充完整。
    证明：延长ED至F'，使DF'＝BF，
    ∵ 四边形ABCD是正方形
    ∴ AB＝AD，∠ABF＝∠ADF'＝90°，
    ∴ △ABF≌△ADF'（SAS）
    应用与拓展：如图建立平面直角坐标系，使顶点A与坐标原点O重合，边OB、OD分别在x轴、y轴的正半轴上。
    （2）设正方形边长OB为30，当E为CD中点时，试问F为BC的几等分点？并求此时F点的坐标；
    （3）设正方形边长OB为30，当EF最短时，直接写出直线EF的解析式：                 。

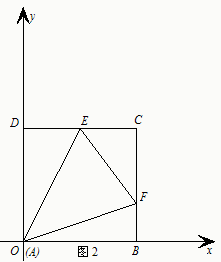
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解：（1）如图①AH=AB

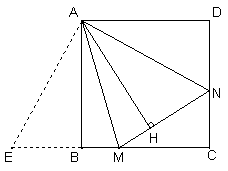
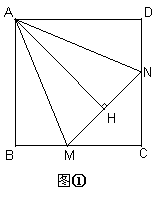    （2）数量关系成立.如图②，延长CB至E，使BE=DN

    ∵ABCD是正方形

    ∴AB=AD，∠D=∠ABE=90°

    ∴Rt△AEB≌Rt△AND

    ∴AE=AN，∠EAB=∠NAD

    ∴∠EAM=∠NAM=45°

    ∵AM=AM

    ∴△AEM≌△ANM

    ∵AB、AH是△AEM和△ANM对应边上的高，

    ∴AB=AH

    （3）如图③分别沿AM、AN翻折△AMH和△ANH，

    得到△ABM和△AND

    ∴BM=2，DN=3，∠B=∠D=∠BAD=90°

    分别延长BM和DN交于点C，得正方形ABCE．

    由（2）可知，AH=AB=BC=CD=AD.                          

      设AH=x，则MC=,  NC=                             图②

    在Rt⊿MCN中，由勾股定理，得

                                        

    ∴

    解得.（不符合题意，舍去）

    ∴AH=6.

    查看答案和解析>>

    同步练习册答案