

分析 (1)将点D的坐标带入抛物线解析式中,利用待定系数法即可求出m的值,再令抛物线解析式中y=0,求出x值,即可得出点A、B的坐标,由此即可得出结论;
(2)过点D作DN⊥AF于点N,交x轴于点M,连接ME,此时ME+MN=DN最小,根据三角形的面积找出关于DN长度的一元一次方程,解方程即可得出结论;
(3)假设存在.根据点A、B、D的坐标可得出△ABD为1:$\sqrt{3}$:2的直角三角形,设出点P、G点的坐标,利用相似三角形的性质即可找出关于m的含绝对值的一元二次方程,解方程即可得出结论.
解答 解:(1)∵点D(2,-$\sqrt{3}$)在抛物线y=$\frac{m}{3}$(x+1)(x-3)(m为常数,且m>0)的图象上,
∴-$\sqrt{3}$=$\frac{m}{3}$(2+1)(2-3),
解得:m=$\sqrt{3}$,
∴抛物线的解析式为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3).
令抛物线y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)中y=0,则有$\frac{\sqrt{3}}{3}$(x+1)(x-3)=0,
解得:x1=-1,x2=3.
∵点A位于点B的左侧,
∴A(-1,0),B(3,0).
故答案为:$\sqrt{3}$;(-1,0).
(2)过点D作DN⊥AF于点N,交x轴于点M,连接ME,此时ME+MN=DN最小,如图1所示.
∵点D(2,-$\sqrt{3}$),∠BAF=∠BAD,
∴点D、E关于x轴对称,
∴点E(2,$\sqrt{3}$),
∵点A(-1,0),
∴AE=$\sqrt{(-1-2)^{2}+(0-\sqrt{3})^{2}}$=2$\sqrt{3}$,DE=2$\sqrt{3}$.
∵S△ADE=$\frac{1}{2}$DE•(xD-xA)=$\frac{1}{2}$AE•DH,
∴DH=3,
∴ME+MN的最小值为3.
(3)假设存在.如图2所示.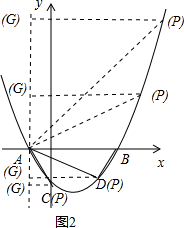
∵A(-1,0),B(3,0),D(2,-$\sqrt{3}$),
∴AB=4,AD=2$\sqrt{3}$,BD=2,
∴△ABD为1:$\sqrt{3}$:2的直角三角形.
∵以P,G,A为顶点的三角形与△ABD相似,
∴∠PGA=∠ADB=90°,
∴$\frac{AG}{PG}$=$\sqrt{3}$或$\frac{PG}{AG}$=$\sqrt{3}$.
设点P(m,$\frac{\sqrt{3}}{3}$(m+1)(m-3)),则点G(-1,$\frac{\sqrt{3}}{3}$(m+1)(m-3)),
∴AG=|$\frac{\sqrt{3}}{3}$(m+1)(m-3)|,PG=|m+1|.
①当$\frac{AG}{PG}$=$\sqrt{3}$时,有|$\frac{\sqrt{3}}{3}$(m+1)(m-3)|=$\sqrt{3}$|m+1|,
解得:m1=0,m2=-1(舍去),m3=6.
此时点P的坐标为(6,7$\sqrt{3}$)或(0,-$\sqrt{3}$);
②当$\frac{PG}{AG}$=$\sqrt{3}$时,有$\sqrt{3}$|$\frac{\sqrt{3}}{3}$(m+1)(m-3)|=|m+1|,
解得:m4=2,m5=-1(舍去),m6=4.
此时点P的坐标为(2,-$\sqrt{3}$)或(4,$\frac{5\sqrt{3}}{3}$).
综上可知:存在点P,使得以P,G,A为顶点的三角形与△ABD相似,点P的坐标为或(0,-$\sqrt{3}$)、(2,-$\sqrt{3}$)、(4,$\frac{5\sqrt{3}}{3}$)或(6,7$\sqrt{3}$).
点评 本题考查了待定系数法求函数解析式、两点间的距离公式、轴对称中的最短路径问题已经相似三角形的性质,解题的关键是:(1)由点的坐标利用待定系数法求函数解析式;(2)确定点M、N的位置;(3)找出关于m的方程.本题属于中档题,难度不大,解决该题型题目时,利用相似三角形的性质找出边与边之间的关系,由边与边之间的关系找出方程是关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:解答题
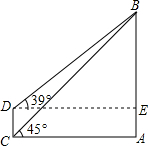 如图:某新电视塔,塔高AB为600米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,求大楼的高度CD(结果精确到1米).
如图:某新电视塔,塔高AB为600米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,求大楼的高度CD(结果精确到1米).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差 | B. | 平均数 | C. | 中位数 | D. | 众数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
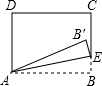 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为$\frac{5}{3}$或15.
如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为$\frac{5}{3}$或15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
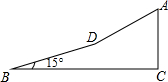 如图,某校八年级(1)班学生利用寒假期间到郊区进行社会实践活动,活动之余,同学们准备攀登附近的一个小山坡,从B点出发,沿坡脚15°的坡面以5千米/时的速度行至D点,用了10分钟,然后沿坡比为1:$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点,用了5分钟,求小山坡的高(即AC的长度)(精确到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732)
如图,某校八年级(1)班学生利用寒假期间到郊区进行社会实践活动,活动之余,同学们准备攀登附近的一个小山坡,从B点出发,沿坡脚15°的坡面以5千米/时的速度行至D点,用了10分钟,然后沿坡比为1:$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点,用了5分钟,求小山坡的高(即AC的长度)(精确到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一面靠墙的空地商用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
如图,在一面靠墙的空地商用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com