
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
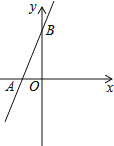
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求直线BP的解析式.
【答案】(1)(-![]() ,0);(0,3);(2)y=x+3或y=-x+3.
,0);(0,3);(2)y=x+3或y=-x+3.
【解析】
试题分析:(1)根据坐标轴上点的坐标特征确定A点和B点坐标;
(2)由OA=![]() ,OP=2OA得到OP=3,分类讨论:当点P在x轴正半轴上时,则P点坐标为(3,0);当点P在x轴负半轴上时,则P点坐标为(-3,0),然后根据待定系数法求两种情况下的直线解析式.
,OP=2OA得到OP=3,分类讨论:当点P在x轴正半轴上时,则P点坐标为(3,0);当点P在x轴负半轴上时,则P点坐标为(-3,0),然后根据待定系数法求两种情况下的直线解析式.
试题解析:(1)把x=0代入y=2x+3,得y═3,
则B点坐标为(0,3);
把y=0代入y=2x+3,得0=2x+3,
解得x=-![]() ,
,
则A点坐标为(-![]() ,0);
,0);
(2)∵OA=![]() ,
,
∴OP=2OA=3,
当点P在x轴正半轴上时,则P点坐标为(3,0),
设直线BP的解析式为:y=kx+b,
把P(3,0),B(0,3)代入得
![]()
解得:![]()
∴直线BP的解析式为:y=-x+3;
当点P在x轴负半轴上时,则P点坐标为(-3,0),
设直线BP的解析式为y=kx+b,
把P(-3,0),B(0,3)代入得
![]()
解得:k=1,b=3
所以直线BP的解析式为:y=x+3;
综上所述,直线BP的解析式为y=x+3或y=-x+3.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=(m+2)x+3-n,
(l)m,n是何值时,y随x的增大而减小?
(2)m,n为何值时,函数的图象经过原点?
(3)若函数图象经过第二、三、四象限,求 m,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:为了求1+3+32+33+…+3100的值,可设M=1+3+32+33+…+3100,则3M=3+32+33+34+…+3101,因此3M﹣M=3101﹣1.所以M=![]() ,
,
即1+3+32+33+…+3100=![]() .问题解决:仿照上述方法求下列式子的值.
.问题解决:仿照上述方法求下列式子的值.
(1)1+4+42+43+…+420.
(2)5101+5102+5103+…+52016.
查看答案和解析>>
科目:初中数学 来源: 题型:
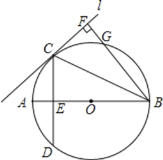
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2m+1)x+m(m+1)=0
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2 , 求x ![]() +x
+x ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某商场因换季,将一品牌服装打折销售,每件服装如果按标价的六折出售将亏10元,而按标价的七五折出售将赚50元,问:
(1) 每件服装的标价是多少元?
(2) 每件服装的成本是多少元?
(3)为保证不亏本,最多能打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
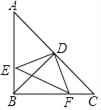
【题目】如图所示,在Rt△ABC中,∠ABC=90°,AB=BC,点D是AC的中点,直角∠EDF的两边分别交AB、BC于点E、F,给出以下结论:①AE=BF;②S四边形BEDF=![]() S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com