
【题目】已知y是关于x的函数,如果能在其函数图象上能找到横坐标与纵坐标相同的一个点P(t,t),则称点P为函数图象上的“郡点”.例如:直线y=2x-1上存在“郡点”P(1,1).
(1)直线y=3x-4的郡点是______;双曲线y=![]() 上的郡点是______.
上的郡点是______.
(2)若抛物线y=x2+5x-5上有“郡点”,且“郡点”A、B(点A,B可重合)的坐标分别为(x1,y1),(x2,y2),求x12+x22的值.
【答案】(1)(2,2);(1,1)和(-1,-1);(2)26
【解析】
(1)由“郡点”的定义可求解;
(2)由“郡点”的定义可得x1=x12+5x1-5,x2=x22+5x2-5,由根与系数关系可求x12+x22的值.
(1)把x=y代入直线y=3x-4,可得x=2=y,
∴直线y=3x-4的郡点是(2,2),
把x=y代入双曲线y=![]() ,可得x1=1,x2=-1,
,可得x1=1,x2=-1,
∴双曲线y=![]() 上的郡点是(1,1),(-1,-1),
上的郡点是(1,1),(-1,-1),
故答案为:(2,2),(1,1),(-1,-1);
(2)∵抛物线y=x2+5x-5上有“郡点”A(x1,y1),B(x2,y2),
可得x1=x12+5x1-5,x2=x22+5x2-5,
因此,x1,x2可看作是方程x=x2+5x-5的两个实数根,
由韦达定理得:x1+x2=-4,x1x2=-5,
∴x12+x22=(x1+x2)2-2x1x2=26.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在湖边高出水面40m的山顶A处看见一架无人机停留在湖面上空某处,观察到无人机底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则无人机底部P距离湖面的高度是( )
A. (40![]() +40)mB. (40
+40)mB. (40![]() +80)mC. (50
+80)mC. (50![]() +100)mD. (50
+100)mD. (50![]() +50)m
+50)m
查看答案和解析>>
科目:初中数学 来源: 题型:
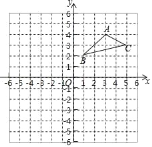
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别是A(3,4)、B(1,2)、C(5,3)
(1)将△ABC平移,使得点A的对应点A1的坐标为(﹣2,4),在如图的坐标系中画出平移后的△A1B1C1;
(2)将△A1B1C1绕点C1逆时针旋转90°,画出旋转后的△A2B2C1并直接写出A2、B2的坐标;
(3)求△A2B2C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3的图象经过点(﹣1,0),(3,0).
(1)求此二次函数的解析式;
(2)在直角坐标系中描点,并画出该函数图象;
x | … | _____ | ____ | ____ | _____ | _____ | … |
y | … | _____ | ____ | ____ | ____ | _____ | … |
(3)根据图象回答:当函数值y<0时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
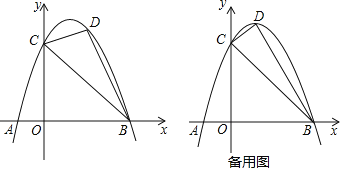
【题目】如图,二次函数![]() 的图象交x轴于A、B两点
的图象交x轴于A、B两点![]() 其中点A在点B的左侧
其中点A在点B的左侧![]() ,交y轴正半轴于点C,且
,交y轴正半轴于点C,且![]() ,点D在该函数的第一象限内的图象上.
,点D在该函数的第一象限内的图象上.
![]() 求点A、点B的坐标;
求点A、点B的坐标;
![]() 若
若![]() 的最大面积为
的最大面积为![]() 平方单位,求点D的坐标及二次函数的关系式;
平方单位,求点D的坐标及二次函数的关系式;
![]() 若点D为该函数图象的顶点,且
若点D为该函数图象的顶点,且![]() 是直角三角形,求此二次函数的关系式.
是直角三角形,求此二次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com