
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点D,直线
轴交于点D,直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点C.
交于点C.
(1)求直线![]() 的解析表达式;
的解析表达式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上存在异于点C的另一点P,使得
上存在异于点C的另一点P,使得![]() 与
与![]() 的面积相等,请求出点P的坐标.
的面积相等,请求出点P的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)P(6,3).
;(3)P(6,3).
【解析】试题分析:(1)利用待定系数法求直线![]() 的解析表达式;
的解析表达式;
(2)由方程组 得到C(2,﹣3),再利用x轴上点的坐标特征确定D点坐标,然后根据三角形面积公式求解;
得到C(2,﹣3),再利用x轴上点的坐标特征确定D点坐标,然后根据三角形面积公式求解;
(3)由于△ADP与△ADC的面积相等,根据三角形面积公式得到点D与点C到AD的距离相等,则D点的纵坐标为3,对于函数![]() ,计算出函数值为3所对应的自变量的值即可得到D点坐标.
,计算出函数值为3所对应的自变量的值即可得到D点坐标.
试题解析:(1)设直线![]() 的解析表达式为
的解析表达式为![]() ,把A(4,0)、B(3,
,把A(4,0)、B(3, ![]() )代入得:
)代入得:  ,解得:
,解得:  ,所以直线
,所以直线![]() 的解析表达式为
的解析表达式为![]() ;
;
(2)解方程组: 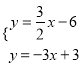 ,得:
,得: ![]() ,则C(2,﹣3);当y=0时,
,则C(2,﹣3);当y=0时, ![]() ,解得x=1,则D(1,0),所以△ADC的面积=
,解得x=1,则D(1,0),所以△ADC的面积=![]() ×(4﹣1)×3=
×(4﹣1)×3=![]() ;
;
(3)因为点D与点C到AD的距离相等,所以D点的纵坐标为3,当y=3时, ![]() ,解得x=6,所以D点坐标为(6,3).
,解得x=6,所以D点坐标为(6,3).


科目:初中数学 来源: 题型:
【题目】己知函数![]() 为反比例函数.
为反比例函数.
己知函数![]() 为反比例函数.
为反比例函数.
![]() 求
求![]() 的值;
的值;
![]() 它的图象在第________象限内,在各象限内,
它的图象在第________象限内,在各象限内,![]() 随
随![]() 增大而________;(填变化情况)
增大而________;(填变化情况)
![]() 当
当![]() 时,此函数的最大值为________,最小值为________.
时,此函数的最大值为________,最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式.例如:![]()
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时, 我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
例如:像![]() ,
,![]() …,这样的分式是假分式;像
…,这样的分式是假分式;像![]() ,
,![]() …,这样
…,这样
的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式.
解决下列问题:
(1)将分式![]() 化为整式与真分式的和的形式为: .(直接写出结果即可)
化为整式与真分式的和的形式为: .(直接写出结果即可)
(2)如果![]() 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,若四边形
,若四边形![]() 、四边形
、四边形![]() 都是正方形,显然图中有
都是正方形,显然图中有![]() ,
,![]() ;
;
![]() 当正方形
当正方形![]() 绕
绕![]() 旋转到如图
旋转到如图![]() 的位置时,
的位置时,![]() 是否成立?若成立,请给出证明;若不成立,请说明理由;
是否成立?若成立,请给出证明;若不成立,请说明理由;
![]() 当正方形
当正方形![]() 绕
绕![]() 旋转到如图
旋转到如图![]() 的位置时,延长
的位置时,延长![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
①求证:![]() ;
;
②当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com