
分析 根据a的值与零的大小关系,可判断开口方向,根据顶点坐标公式,可得对称轴、顶点坐标;由此逐一得出答案即可.
解答 解:(1)y=-2x2+8x-7,a=-2<0,抛物线开口向下,对称轴是x=-$\frac{8}{2×(-2)}$=2,顶点横坐标是2,顶点的纵坐标是$\frac{4×(-2)×(-7)-{8}^{2}}{4×(-2)}$=1,顶点坐标是(2,1);
(2)y=2x2+4x+1,a=2>0,抛物线开口向上,对称轴是x=-2,顶点横坐标是=-2,顶点的纵坐标是$\frac{4×2×1-{4}^{2}}{4×2}$=-1,顶点坐标是(-2,-1);
(3)y=-x2-2x-2,a=-1<0,抛物线开口向下,对称轴是x=-1,顶点横坐标是-1,顶点的纵坐标是$\frac{4×(-1)×(-2)-(-2)^{2}}{4×(-1)}$=-1,顶点坐标是(-1,-1);
(4)y=-$\frac{1}{2}$x2+3x,a=-$\frac{1}{2}$<0,抛物线开口向下,对称轴是x=3,顶点横坐标是3,顶点的纵坐标是$\frac{{-3}^{2}}{-2}$=$\frac{9}{2}$,顶点坐标是(3,$\frac{9}{2}$).
点评 本题考查了二次函数的性质,a>0,抛物线开口向上,对称轴是x=-$\frac{b}{2a}$,顶点横坐标是=-$\frac{b}{2a}$,顶点的纵坐标是$\frac{4ac-{b}^{2}}{4a}$,顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$).


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
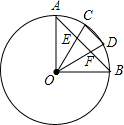 如图,扇形OAB的圆心角为90°,C、D是$\widehat{AB}$的三等分点,AB与OC、OD分别相交于点E、F.指出图中与AE相等的线段,并说明理由.
如图,扇形OAB的圆心角为90°,C、D是$\widehat{AB}$的三等分点,AB与OC、OD分别相交于点E、F.指出图中与AE相等的线段,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
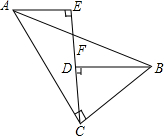 如图,∠ACB=90°,AC=BC,F为AB上一点,BD⊥CF于D,AE⊥CF交CF的延长线于E,猜想BD,AE,ED之间的数量关系,并说明理由.
如图,∠ACB=90°,AC=BC,F为AB上一点,BD⊥CF于D,AE⊥CF交CF的延长线于E,猜想BD,AE,ED之间的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
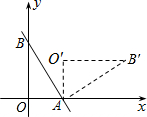 如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则直线AB′的函数解析式是y=0.5x-0.5.
如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则直线AB′的函数解析式是y=0.5x-0.5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com