
 如图,已知△ABC中,∠C=90°,E、F在AB边上,AF=EF=EB,且CF=sinα,CE=cosα,求斜边AB的长.
如图,已知△ABC中,∠C=90°,E、F在AB边上,AF=EF=EB,且CF=sinα,CE=cosα,求斜边AB的长. 分析 延长CF到G,使FG=CF=3,连接EG并延长交AC与H,作DF⊥HG,由SAS定理得出△EFG≌△BFC,故EG=BC,∠G=∠BCF,同理可得△AHE≌△FDE,DF=AH,由平行线分线段成比例可知,HC=2DF,BC=3HE,设DF=AH=a,ED=EH=b,则HC=2a,EG=BC=3b,则DG=3b-b=2b,在Rt△CHE和Rt△FDG中根据勾股定理可知(2a)2+b2=cos2α①,(2b)2+a2=sin2α②,两式相加可得出EF的长,进而得出结论.
解答 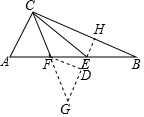 解:延长CF到G,使FG=CF=3,连接EG并延长交BC与H,作DF⊥HG,
解:延长CF到G,使FG=CF=3,连接EG并延长交BC与H,作DF⊥HG,
在△EFG与△AFC中,
∵$\left\{\begin{array}{l}{EF=FA}\\{∠EFG=∠CFA}\\{CF=FG}\end{array}\right.$
∴△EFG≌△AFC(SAS),
∴EG=AC,∠G=∠ACF,
∴GH∥AC,
∴GH⊥BC,
∴DF∥BC,
同理可得△BHE≌△FDE,
∴DF=BH,
由平行线分线段成比例可知,HC=2DF,AC=3HE,
设DF=BH=a,ED=EH=b,则HC=2a,EG=BC=3b,
∴DG=3b-b=2b,
在Rt△CHE和Rt△FDG中,(2a)2+b2=cos2α①,(2b)2+a2=sin2α②,
①+②得,a2+b2=$\frac{1}{5}$,即EF2=$\frac{1}{5}$,解得EF=$\frac{\sqrt{5}}{5}$,
∴AB=3EF=$\frac{3\sqrt{5}}{5}$.
点评 本题考查的是勾股定理,根据题意作出辅助线,构造出全等三角形是解答此题的关键.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
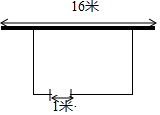 现有32米长的栅栏在长16米的墙边围成面积为130平方米的一个矩形的堆料场.在墙的对面的一边留出1米宽的进出口(如图).这个矩形的长和宽各是多少米?
现有32米长的栅栏在长16米的墙边围成面积为130平方米的一个矩形的堆料场.在墙的对面的一边留出1米宽的进出口(如图).这个矩形的长和宽各是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
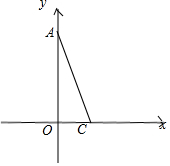 如图,△ABC在平面坐标系内,点A(0,3$\sqrt{3}$),C(2,0).点B为y轴上动点,求$\frac{1}{2}$AB+BC的最小值.
如图,△ABC在平面坐标系内,点A(0,3$\sqrt{3}$),C(2,0).点B为y轴上动点,求$\frac{1}{2}$AB+BC的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
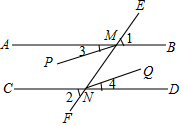 如图,直线EF分别交AB,CD于M,N,且∠1=∠2,∠3=∠4
如图,直线EF分别交AB,CD于M,N,且∠1=∠2,∠3=∠4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
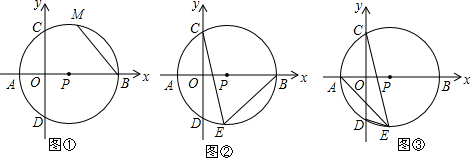
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com