
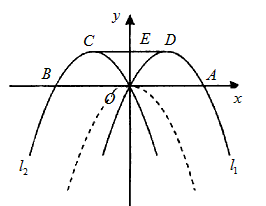
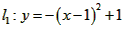 (或
(或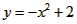 );
);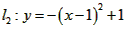 (或
(或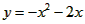 );
);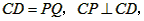 ,四边形CPQD是矩形,
,四边形CPQD是矩形,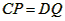 (或CQ=DP),但CD≠PQ,
(或CQ=DP),但CD≠PQ,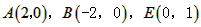 ,
,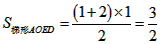
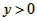 时,
时,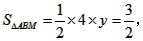
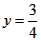
 代入l1的解析式,解得:
代入l1的解析式,解得: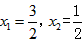 ,
,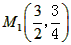 ,
,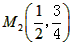
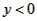 时,
时,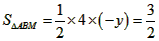
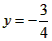 ,
,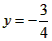 代入l1的解析式,解得:
代入l1的解析式,解得: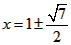 ,
,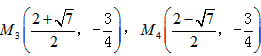 。
。

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
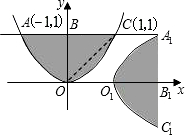 如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的是( )
如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的是( )| A、点O1的坐标是(1,0) | B、点C1的坐标是(2,-1) | C、四边形OBA1B1是矩形 | D、若连接OC,则梯形OCA1B1的面积是3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 标;如果不存在,请说明理由.
标;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
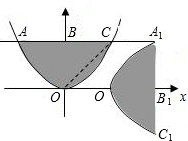 如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的有( )个.
如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的有( )个.| A、2 | B、3 | C、4 | D、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•广安)如图,把抛物线y=
(2012•广安)如图,把抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
| 27 |
| 2 |
| 27 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com