【题目】已知：四边形ABCD的对角线AC、BD相交于点O，给出下列4个条件：①AB∥CD；②OA＝OC；③AB＝CD；④AD∥BC从中任取两个条件，能推出四边形ABCD是平行四边形的概率是( )
A. 
B. 
C. 
D. 
科目：初中数学 来源： 题型：
【题目】如图1，在ABCD中，AE⊥BC于E，E恰为BC的中点．tanB＝2．
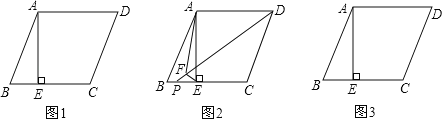
（1）求证：AD＝AE；
（2）如图2．点P在BE上，作EF⊥DP于点F，连结AF．线段DF、EF与AF之间有怎样的数量关系？并说明理由；
（3）请你在图3中画图探究：当P为射线EC，上任意一点（P不与点E重合）时，作EF⊥DP于点F，连结AF，线段DF、EF与AF之间有怎样的数量关系？请在图3中补全图形，直接写出结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD，∠BED＝60°，∠ABE的角平分线与∠CDE的角平分线交于点F，则∠DFB＝（ ）
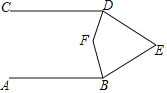
A. 150°B. 120°C. 100°D. 135°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知ABCD，点E是BC边上的一点，将边AD延长至点F，使∠AFC＝∠DEC.
(1)求证：四边形DECF是平行四边形；
(2)若AB＝13，DF＝14，tan A＝
，求CF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线y=ax2-2ax-3a（a≠0）顶点为P，且该抛物线与x轴交于A，B两点（点A在点B的左侧）．我们规定：抛物线与x轴围成的封闭区域称为“G区域”（不包含边界）；横、纵坐标都是整数的点称为整点．
（1）求抛物线y=ax2-2ax-3a顶点P的坐标（用含a的代数式表示）；
（2）如果抛物线y=ax2-3ax-3a经过（1，3）．
①求a的值；
②在①的条件下，直接写出“G区域”内整点的个数．
（3）如果抛物线y=ax2-2ax-3a在“G区域”内有4个整点，直接写出a的取值范围．
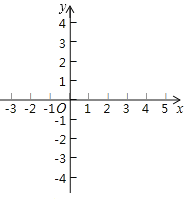
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年“五一”假期，某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点，再从B点沿斜坡BC到达山顶C点，路线如图所示.斜坡AB的长为1000米，斜坡BC的长为200
米，在C点测得B点的俯角为45°，已知A点海拔21米，C点海拔721米.
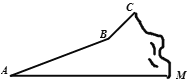
(1)求B点的海拔；
(2)求斜坡AB的坡角.
查看答案和解析>>
科目：初中数学 来源： 题型：
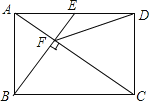
【题目】如图，在矩形ABCD中，E是AD边上的中点，BE⊥AC于F，连接DF，下列4个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④tan∠CAD＝
，其中结论正确的序号是______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE．
（1）求证：四边形ABCD是菱形；
（2）若AB＝
，BD＝2，求OE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
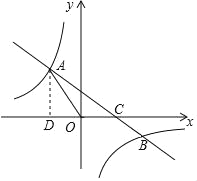
【题目】如图，在平面直角坐标系xOy中，一次函数y＝kx+b(k≠0)的图象与反比例函数y＝
(n≠0)的图象交于第二、四象限内的A、B两点，与x轴交于点C，点B 坐标为(m，﹣1)，AD⊥x轴，且AD＝3，tan∠AOD＝
．
(1)求该反比例函数和一次函数的解析式；
(2)求△AOB的面积；
(3)点E是x轴上一点，且△AOE是等腰三角形，请直接写出所有符合条件的E点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
