

���� ��1�����õȱ������ε����ʿ�֤����APC�ա�BQA�������á�BAQ=��ACP����������������ǵ����ʿ�֤�á�CMQ=60�㣻
��2������t�ֱ��ʾ��BP��BQ���֡�BPQ=90��͡�BPQ=90������������ֱ�����ֱ�������ε����ʿɵõ�����t�ķ��̣�������t��ֵ��
��3��ͬ��1����֤�á�PBC�ա�QCA����������������ǵ����ʿ���á�CMQ=120�㣮
��� �⣺
��1���ߡ�ABCΪ�ȱ������Σ�
��AB=AC����B=��PAC=60�㣬
�ߵ�P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s��
��AP=BQ��
�ڡ�APC�͡�BQA��
$\left\{\begin{array}{l}{AP=BQ}\\{��PAC=��B}\\{AC=AB}\end{array}\right.$
���APC�ա�BQA��SAS����
���BAQ=��ACP��
���CMQ=��CAQ+��ACP=��BAQ+��CAQ=��BAC=60�㣬
����P��Q�˶��Ĺ����У���CMQ���䣬��CMQ=60�㣻
��2�����˶�ʱ��Ϊts����AP=BQ=t��
��PB=4-t��
����PQB=90��ʱ��
�ߡ�B=60�㣬
��PB=2BQ��
��4-t=2t�����t=$\frac{4}{3}$��
����BPQ=90��ʱ��
�ߡ�B=60�㣬
��BQ=2PB��
��t=2��4-t�������t=$\frac{8}{3}$��
�൱tΪ$\frac{4}{3}$s��$\frac{8}{3}$s ʱ����PBQΪֱ�������Σ�
��3���ڵȱ�������ABC�У�AC=BC����ABC=��BCA=60�㣬
���PBC=��QCA=120�㣬��BP=CQ��
�ڡ�PBC�͡�QCA��
$\left\{\begin{array}{l}{PB=CQ}\\{��PBC=��ACQ}\\{AC=BC}\end{array}\right.$
���PBC�ա�QCA��SAS����
���BPC=��MQC��
�֡ߡ�PCB=��MCQ��
���CMQ=��PBC=120�㣬
����P��Q�˶��Ĺ����У���CMQ�Ĵ�С���䣬��CMQ=120�㣮
���� ����Ϊ�����ε��ۺ�Ӧ�ã��漰�ȱ������ε����ʡ�ֱ�������ε����ʡ����ɶ�����ȫ�������ε��ж������ʡ���ǵ����ʡ���������˼�뼰����˼���֪ʶ���ڣ�1������3����֤��������ȫ���ǽ���Ĺؼ����ڣ�2������ֱ�������ε����ʵõ�����t�ķ����ǽ���Ĺؼ���ע���������������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڱ߳�Ϊ1��������ABCD�У���A������Ϊ��1��1����AD��x�ᣬ����P��B��A��D��C��B�˶����Ե�PΪ�����������y=ax2+bx+c��a��0����x����M��N���㣨��M�ڵ�N����ߣ�������P�˶�ʱ������������֮ƽ�ƣ�����M�ĺ��������СֵΪ-1�����N�ĺ���������ֵΪ4��
��ͼ���ڱ߳�Ϊ1��������ABCD�У���A������Ϊ��1��1����AD��x�ᣬ����P��B��A��D��C��B�˶����Ե�PΪ�����������y=ax2+bx+c��a��0����x����M��N���㣨��M�ڵ�N����ߣ�������P�˶�ʱ������������֮ƽ�ƣ�����M�ĺ��������СֵΪ-1�����N�ĺ���������ֵΪ4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
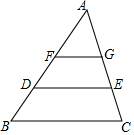 ��ͼ���ڡ�ABC�У���֪FG��DE��BC����FG��DE�ѡ�ABC��������ȷ֣���FG��DE��BC��ֵ��
��ͼ���ڡ�ABC�У���֪FG��DE��BC����FG��DE�ѡ�ABC��������ȷ֣���FG��DE��BC��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com