
����Ŀ��ij�Ľ���Ʒ�̵�������![]() ���ֱʼDZ�����
���ֱʼDZ�����![]() Ԫ������
Ԫ������![]() �ֱʼDZ�����
�ֱʼDZ�����![]() Ԫ������
Ԫ������![]() �ֱʼDZ���������ͬ��ÿ��
�ֱʼDZ���������ͬ��ÿ��![]() �ֱʼDZ��Ľ��۱�ÿ��
�ֱʼDZ��Ľ��۱�ÿ��![]() �ֱʼDZ��Ľ��۹�
�ֱʼDZ��Ľ��۹�![]() Ԫ��
Ԫ��
��1����![]() ���ֱʼDZ�ÿ���Ľ��۷ֱ�Ϊ����Ԫ?
���ֱʼDZ�ÿ���Ľ��۷ֱ�Ϊ����Ԫ?
��2�������̵�![]() �ֱʼDZ�ÿ���ۼ�
�ֱʼDZ�ÿ���ۼ�![]() Ԫ��
Ԫ��![]() �ֱʼDZ�ÿ���ۼ�
�ֱʼDZ�ÿ���ۼ�![]() Ԫ��������
Ԫ��������![]() ���ֱʼDZ���
���ֱʼDZ���![]() �����������ֱʼDZ�ȫ���۳����ܻ���������
�����������ֱʼDZ�ȫ���۳����ܻ���������![]() Ԫ��������
Ԫ��������![]() �ֱʼDZ����ٱ�?.
�ֱʼDZ����ٱ�?.
���𰸡���1��A�ֱʼDZ�ÿ���Ľ���Ϊ30Ԫ��B�ֱʼDZ�ÿ���Ľ���Ϊ40Ԫ����2������A�ֱʼDZ�28����
��������
��1����A�ֱʼDZ�ÿ���Ľ���ΪxԪ����B�ֱʼDZ�ÿ���Ľ���Ϊ(x+10)Ԫ����������=�ܼۡµ��۽����150Ԫ������A�ֱʼDZ�����200Ԫ������B�ֱʼDZ�������ͬ�����ɵó�����x�ķ�ʽ���̣���֮������ɵó����ۣ�
��2���蹺��A�ֱʼDZ�m������B�ֱʼDZ�(80��m)��������������=ÿ�����������������(��������)����ܻ�����С��372Ԫ�����ɵó�����m��һԪһ�β���ʽ����֮ȡ���е����ֵ���ɵó����ۣ�
��1����A�ֱʼDZ�ÿ���Ľ���ΪxԪ����B�ֱʼDZ�ÿ���Ľ���Ϊ(x+10)Ԫ��
�����⣬�ã�![]() ��
��
��ã�x=30��
�����飬x=30��ԭ���̵Ľ⣬�ҷ������⣬
��x=30ʱ��x+10=40��
��A�ֱʼDZ�ÿ���Ľ���Ϊ30Ԫ��B�ֱʼDZ�ÿ���Ľ���Ϊ40Ԫ��
��2���蹺��A�ֱʼDZ�m������B�ֱʼDZ�(80��m)����
�����⣬�ã�(34��30)m+(45��40)(80��m)��372��
��ã�m��28��
������A�ֱʼDZ�28����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������չ����������й�����ֲ�ѳ��߹�ģ��������������ˮ�����ص�Ӱ�죬���ҽ�ȥ����С���ȵļ���������������������
��1������ij��ũ�����ջ���Һ����˹�![]() ǧ�ˣ��������˵IJ���������ӣ�Ҳ�����
ǧ�ˣ��������˵IJ���������ӣ�Ҳ�����![]() ������ù�ũ�����ջ�ӣ�����ٶ���ǧ�ˣ�
������ù�ũ�����ջ�ӣ�����ٶ���ǧ�ˣ�
��2���ù�ũ�ѽ����ջ��ӣ�ҡ���������ˮ����һ���������г����ۣ��ù�ũȥ����ҵ��г�������Ϊ![]() ǧ�ˣ����۾���Ϊ
ǧ�ˣ����۾���Ϊ![]() Ԫǧ�ˣ�����ӣ�ҵ��г���������ȥ�������
Ԫǧ�ˣ�����ӣ�ҵ��г���������ȥ�������![]() �����۾��۱�ȥ������
�����۾��۱�ȥ������![]() ���ù�ũȥ�����˵��г�������Ϊ
���ù�ũȥ�����˵��г�������Ϊ![]() ǧ�ˣ����۾���Ϊ
ǧ�ˣ����۾���Ϊ![]() Ԫǧ�ˣ��������˵��г���������ȥ��������
Ԫǧ�ˣ��������˵��г���������ȥ��������![]() �������۾��۱�ȥ�������
�������۾��۱�ȥ�������![]() ���ù�ũ���������г����۵��ⲿ�֙��Һ����˵������ܽ������ȥ����Һ����˵��г������ܽ����ͬ����
���ù�ũ���������г����۵��ⲿ�֙��Һ����˵������ܽ������ȥ����Һ����˵��г������ܽ����ͬ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
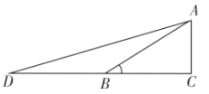
����Ŀ����ͼ����ABCΪ�ȱ������Σ�AB��3������PΪ��ABC��һ���㣬�������PAB����ACP�����߶�PB���ȵ���СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2+bx+c�ĶԳ���Ϊx����1���ҹ��㣨��3��0������0����3����
��1���������ߵı���ʽ��
��2����֪�㣨m��k���͵㣨n��k���ڴ��������ϣ�����m��n�����жϹ���t�ķ���t2+mt+n��0�Ƿ���ʵ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ����
�Ķ����⣺��ѧ��ȤС����̽�������![]() ��ֵ������˼�������ۡ��������õ�����˼·��
��ֵ������˼�������ۡ��������õ�����˼·��
��ͼ1����![]() ��ʹ
��ʹ![]() ��
��![]() ���ӳ�
���ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() ������
������![]() .
.
��![]() ����
����![]() ��
��![]() .
.![]()
![]() .
.
�����������⣺
��1�������⣺���![]() ��ֵ��
��ֵ��
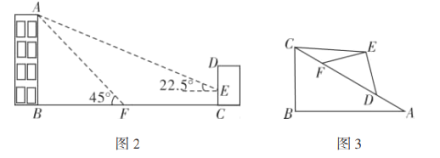
��2������������ͼ2��ijסլ¥![]() �ĺ�����һ������
�ĺ�����һ������![]() �������������ļн���
�������������ļн���![]() ʱ��סլ�ڽ������ǽ�����¸�
ʱ��סլ�ڽ������ǽ�����¸�![]() ��Ӱ��
��Ӱ��![]() ���������������ļн���
���������������ļн���![]() ʱ��סլ¥��
ʱ��סլ¥��![]() �ڵ����ϵ�Ӱ��
�ڵ����ϵ�Ӱ��![]() ��ǽ��
��ǽ��![]() ��
��![]() �ľ��루
�ľ��루![]() ��
��![]() ��
��![]() ��һ��ֱ���ϣ�.��סլ¥
��һ��ֱ���ϣ�.��סլ¥![]() �ĸ߶ȣ�����������ţ���
�ĸ߶ȣ�����������ţ���
��3��̽�����֣���ͼ3��С����ӲֽƬ��������ֱ�������Σ���![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() .����
.����![]() ���
���![]() ��
��![]() ���
��б��![]() �غ���һ�𣬲���
�غ���һ�𣬲���![]() ��
��![]() �����ƶ�.���ƶ������У�
�����ƶ�.���ƶ������У�![]() ��
��![]() ����ʼ����
����ʼ����![]() ���ϣ��ƶ���ʼʱ��
���ϣ��ƶ���ʼʱ��![]() ���
���![]() �غϣ�.̽����
�غϣ�.̽����![]() �ƶ������У��Ƿ����ij��λ�ã�ʹ��
�ƶ������У��Ƿ����ij��λ�ã�ʹ��![]() ��������ڣ�ֱ��д��
��������ڣ�ֱ��д��![]() �ij��ȣ���������ڣ���˵������.
�ij��ȣ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
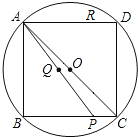
����Ŀ����ͼ��![]() �ڽ��ڡ�O��
�ڽ��ڡ�O��![]() ��
��![]() �ǡ�O�����
�ǡ�O�����![]() ����Բ��
����Բ��![]() �����ĶԳƵĵ㣬
�����ĶԳƵĵ㣬![]() ��
��![]() ����һ�㣬����
����һ�㣬����![]() ����֪
����֪![]() ��
��![]() ��
��![]() ���߶�
���߶�![]() ��һ���㣬����
��һ���㣬����![]() ���ӳ����ı���
���ӳ����ı���![]() ��һ���ڵ�
��һ���ڵ�![]() ��������
��������![]() ����
����![]() ��ֵΪ_______________��
��ֵΪ_______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���D��E��BC���ϣ���F��AC���ϣ�����ABD����AD���ۣ�ʹ��B�͵�E�غϣ�����CEF����EF���ۣ���Cǡ���A�غϣ����ۣ��١�BAC=90������DE=EF���ۡ�B=2��C����AB=EC����ȷ���У�������
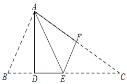
A.�٢ڢۢ�B.�ۢ�C.�٢ڢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
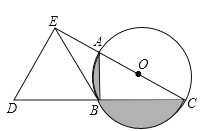
����Ŀ����ͼ��ACΪ��O��ֱ����BΪ��O��һ�㣬��ACB=30�㣬�ӳ�CB����D��ʹ��CB=BD������D��DE��AC������E��CA���ӳ����ϣ�����BE��
��1����֤��BE����O�����ߣ�
��2����BE=3ʱ����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
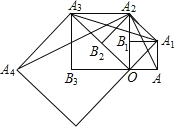
����Ŀ����ͼ���ı��� OAA1B1 �DZ߳�Ϊ 1 �������Σ��ԶԽ��� OA1 Ϊ�����ڶ��������� OA1A2B2������ AA2���õ��� AA1A2�����ԶԽ��� OA2 Ϊ���������������� OA2A3B3������ A1A3���õ���A1A2A3�����ԶԽ��� OA3 Ϊ������ �ĸ������Σ����� A2A4���õ���A2A3A4�����ǡ�AA1A2����A1A2A3����A2A3A4 ������ֱ�Ϊ S1��S2��S3������� ȥ���� S2019��_____ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com