
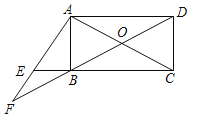
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据AE2=EBEC证明△AEB∽△CEA,即可得到∠EBA=∠EAC=90°,从而说明平行四边形ABCD是矩形;
(2)根据(1)中△AEB∽△CEA可得![]() ,再证明△EBF∽△BAF可得
,再证明△EBF∽△BAF可得![]() ,结合条件AF=AC,即可证AE=BF.
,结合条件AF=AC,即可证AE=BF.
证明:(1)∵AE2=EBEC
∴![]()
又∵∠AEB=∠CEA
∴△AEB∽△CEA
∴∠EBA=∠EAC
而∠EAC=90°
∴∠EBA=∠EAC=90°
又∵∠EBA+∠CBA=180°
∴∠CBA=90°
而四边形ABCD是平行四边形
∴四边形ABCD是矩形
即得证.
(2)∵△AEB∽△CEA
∴![]() 即
即![]() ,∠EAB=∠ECA
,∠EAB=∠ECA
∵四边形ABCD是矩形
∴OB=OC
∴∠OBC=∠ECA
∴∠EBF=∠OBC=∠ECA=∠EAB
即∠EBF=∠EAB
又∵∠F=∠F
∴△EBF∽△BAF
∴![]()
∴![]()
而AF=AC
∴BF=AE
即AE=BF得证.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=CD=5厘米,AD=BC=4厘米.动点P从A出发,以1厘米/秒的速度沿A→B运动,到B点停止运动;同时点Q从C点出发,以2厘米/秒的速度沿C→B→A运动,到A点停止运动.设P点运动的时间为t秒(t>0),

(1)当点Q在BC边上运动时,t为何值,AP=BQ;
(2)当t为何值时,S△ADP=S△BQD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店开展优惠售书活动,一次购书定价不超过200元的打九折;一次购书定价超过200元的,其中200元按九折计算,超过200元的部分打八折.小丽挑选了几本喜爱的书,计算定价后,准备支付144元,遇见同学小芳也在买书,计算小芳购书的定价后,小丽对小芳说:我们独自付款,都只能享受九折,合在一-起付款,按今天的活动一共可优惠 48元.请根据以上内容解答下列问题:
(1)小丽购书的定价是____元 .
(2)列方程求解小芳购书的定价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上(与
上(与![]() 、
、![]() 不重合),四边形
不重合),四边形![]() 为正方形,过点
为正方形,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,对于下列结论:①
,对于下列结论:①![]() ;②四边形
;②四边形![]() 是矩形;③
是矩形;③![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
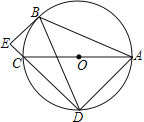
【题目】如图,⊙O是△ABC的外接圆,AC为直径,BD=BA,BE⊥DC交DC的延长线于点E
(1) 求证:BE是⊙O的切线
(2) 若EC=1,CD=3,求cos∠DBA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小靓用七巧板拼成一幅装饰图,放入长方形ABCD内,装饰图中的三角形顶点E,F分别在边AB,BC上,三角形①的边GD在边AD上,若图1正方形中MN=1,则CD=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )

A.AC=BD B.AB=AC C.∠ABC=90°D.AC⊥BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com