
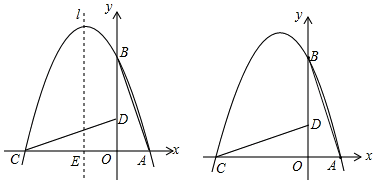
分析 (1)由条件可求得A、B、C三点的坐标分别为(1,0)、(0,3)、C(-3,0),代入解析式可求得抛物线的解析式;
(2)①若△CEF与△COD相似,则有∠CFE=90°或∠CEF=90°,当∠CFE=90°时,连接PE并延长交y轴于点H,根据题意可证明△ODC≌△OEH,则OH=OC,可求得Q的坐标,结合E点坐标,可求出直线PH的解析式,联立直线和抛物线的解析式可求得P点坐标;当∠CEF=90°时,可知P点为抛物线的顶点;②连接AD并延长,交抛物线于点P,连接PB,可证得PB∥x轴,则可知∠APB=45°,满足条件.
解答 解:
(1)∵tan∠BAO=$\frac{BO}{AO}$,
∴$\frac{BO}{1}$=3,解得BO=3,
又由旋转可得OC=OB=3,
∴A、B、C三点的坐标分别为(1,0)、(0,3)、C(-3,0),
代入二次函数解析式可得$\left\{\begin{array}{l}{a+b+c=0}\\{9a-3b+c=0}\\{c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$.
∴抛物线的解析式为:y=-x2-2x+3;
(2)①∵∠DOC=90°,
∴当△CEF与△COD相似,有∠CFE=90°或∠CEF=90°,
当∠CFE=90°时,连接PE并延长交y轴于点H,如图1,
由题意可知l方程为x=-1,∴OD=OE,
∵∠DCO+∠CDO=∠CDO+∠EHO=90°,
∴∠DCO=∠EHO,
在△ODC和△OEH中,
$\left\{\begin{array}{l}{∠DCO=∠EHO}\\{∠DOC=∠EOH}\\{DO=EO}\end{array}\right.$
∴△ODC≌△OEH(AAS),
∴OH=OC=3,
∴H坐标为(0,-3),且E(-1,0),
设直线PH解析式为y=kx-3,把E点坐标代入可得-k-3=0,解得k=-3,
∴直线PH解析式为y=-3x-3,
联立抛物线线解析式可得$\left\{\begin{array}{l}{y=-{x}^{2}-2x+3}\\{y=-3x-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=-12}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$,
∵P点在第二象限,
∴P点坐标为(-2,3);
当∠CEF=90°时,则PE∥y轴,故P点坐标为抛物线的顶点,可求得P点坐标为(-1,4);
综上可知当△CEF与△COD相似时点P的坐标为(-2,3)或(-1,4);
②如图2,连接AD并延长,交抛物线于点P,连接PB,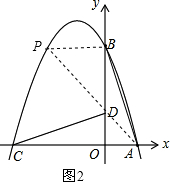
∵A(1,0),D(0,1),
∴直线AD解析式为y=-x+1,
联立直线AD和抛物线解析式可得$\left\{\begin{array}{l}{y=-x+1}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$,
∴P(-2,3),且B(0,3),
∴PB∥x轴,
∴∠APB=∠DAO=45°,
∴当∠BAP=45°时,P点坐标为(-2,3).
点评 本题为二次函数的综合应用,涉及待定系数法、全等三角形的判定和性质、相似三角形的判定和性质、函数图象的交点及方程思想等知识.在(1)中注意待定系数示的应用,关键是确定点的坐标,在(2)①中利用相似求得直线PE于y轴的交点坐标是解题的关键,注意方程思想的应用,在(2)②中确定出点P的位置是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
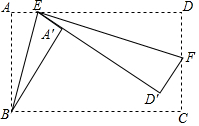 如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为$\frac{15+\sqrt{33}}{3}$或$\frac{15-\sqrt{33}}{3}$.
如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为$\frac{15+\sqrt{33}}{3}$或$\frac{15-\sqrt{33}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°查看答案和解析>>
科目:初中数学 来源: 题型:填空题
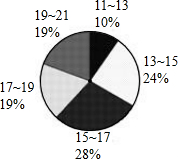 某大型网店为了对网上促销员建立销售业绩管理制度,随机抽取了部分促销员,统计了他们的月平均销售业绩(单位:万元),制作了如图的扇形统计图.如果要使半数左右的促销员都能达到业绩目标,则每个促销员最合适的月销售额目标应该定为16万左右.(结果取整数)
某大型网店为了对网上促销员建立销售业绩管理制度,随机抽取了部分促销员,统计了他们的月平均销售业绩(单位:万元),制作了如图的扇形统计图.如果要使半数左右的促销员都能达到业绩目标,则每个促销员最合适的月销售额目标应该定为16万左右.(结果取整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4×108 | B. | 4×10-8 | C. | 0.4×108 | D. | -4×108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com