
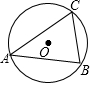
 如图,⊙O为△ABC的外接圆,∠ACB=75°,∠BAC=45°,⊙O的半径为$\sqrt{2}$,若点P与点C的距离为1,则△ABP的面积S的取值范围是( )
如图,⊙O为△ABC的外接圆,∠ACB=75°,∠BAC=45°,⊙O的半径为$\sqrt{2}$,若点P与点C的距离为1,则△ABP的面积S的取值范围是( )| A. | 1≤S≤2+$\sqrt{3}$ | B. | 1≤S≤1+$\sqrt{3}$ | C. | $\sqrt{3}$-1≤S≤$\sqrt{3}$+1 | D. | $\sqrt{3}$+1≤S≤$\sqrt{3}$+2 |
分析 过C点作CH⊥AB于H,交⊙C于E1、E2点,则E点运动到E1点时S最小,E点运动到E2点时S最大,易得△ACH为等腰直角三角形,则AH=CH=$\sqrt{3}$,∠ACH=45°,
再由∠ACB=75°得∠BCH=30°,根据含30°的直角三角形三边的关系得BH=$\frac{\sqrt{3}}{3}$CH=1,AB=$\sqrt{3}$+1,则HE1=$\sqrt{3}$-1,HE2=$\sqrt{3}$+1,然后根据三角形面积公式即可解决问题.
解答 解:以C为圆心1为半径作⊙C,过C点作CH⊥AB于H,交⊙C于E1、E2点,则E点运动到E1点时S最小,E点运动到E2点时S最大, 连接OC、OB
连接OC、OB
∵∠BAC=45°,
∴△ACH为等腰直角三角形,∠BOC=90°,
BC=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2,
在Rt△BHC中,∵∠CHB=90°,∠B=180°-∠BAC-∠ACB=60°,
∴∠BCH=30°,
∴BH=$\frac{1}{2}$BC=1,CH=AH=$\sqrt{3}$,AB=1+$\sqrt{3}$,
∵HE1=CH-CE1=$\sqrt{3}$-1,HE2=CH+CE2=$\sqrt{3}$+1,
∴△ABE1的面积=$\frac{1}{2}$×( $\sqrt{3}$-1)×( $\sqrt{3}$+1)=1,△ABE2的面积=$\frac{1}{2}$×( $\sqrt{3}$+1)×( $\sqrt{3}$+1)=2+$\sqrt{3}$,
∴1≤S≤2+$\sqrt{3}$.
故选A.
点评 本题考查了圆的综合题:熟练运用圆的有关性质进行几何计算;含30°的直角三角形和等腰直角三角形三边的关系要记住.


科目:初中数学 来源: 题型:填空题
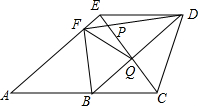 如图,四边形ACDE是梯形,四边形ABDE是平行四边形;点F在边AE上,DF、DB分别交CE于P、Q,如果△QCD的面积是30,△PDQ和△PEF的面积之差为16,那么四边形ABQF的面积是76.
如图,四边形ACDE是梯形,四边形ABDE是平行四边形;点F在边AE上,DF、DB分别交CE于P、Q,如果△QCD的面积是30,△PDQ和△PEF的面积之差为16,那么四边形ABQF的面积是76.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
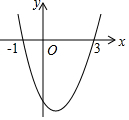 已知二次函数y=ax2+bx+c的图象如图,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b-2a=0,②abc<0,③2a-3b+4c<0,④8a+c>0,其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b-2a=0,②abc<0,③2a-3b+4c<0,④8a+c>0,其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com