
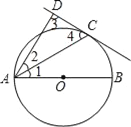
【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于C点,AC平分∠DAB.
(1)求证:AD⊥CD;
(2)若AD=2, ![]() ,求⊙O的半径R的长.
,求⊙O的半径R的长.
【答案】(1)证明见解析;(2)⊙O的半径R的长为![]() .
.
【解析】试题分析:(1)连接OC,由题意得OC⊥CD.又因为AC平分∠DAB,则∠1=∠2=![]() ∠DAB.即可得出AD∥OC,则AD⊥CD;
∠DAB.即可得出AD∥OC,则AD⊥CD;
(2)连接BC,则∠ACB=90°,可证明△ADC∽△ACB.则![]() ,从而求得R.
,从而求得R.
试题解析:(1)证明:连接OC,

∵直线CD与⊙O相切于C点,AB是⊙O的直径,
∴OC⊥CD.
又∵AC平分∠DAB,
∴∠1=∠2=![]() ∠DAB.
∠DAB.
又∠COB=2∠1=∠DAB,
∴AD∥OC,
∴AD⊥CD.
(2)连接BC,则∠ACB=90°,
在△ADC和△ACB中
∵∠1=∠2,∠3=∠ACB=90°,
∴△ADC∽△ACB.
∴![]()
∴R=![]()


科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论: ①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .
.
其中正确的序号是(把你认为正确的都填上).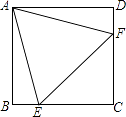
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n满足等式(m﹣8)2+2|n﹣m+5|=0.
(1)求m,n的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=nPB,点Q为PB的中点,求线段AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB为锐角,如图(1).
(1)若OM平分∠AOC,ON平分∠BOD,∠MON=32°,∠COD=10°,如图(2)所示,求∠AOB的度数.
(2)若OM,OD,OC,ON是∠AOB的五等分线,如图(3)所示,以射线OA,OM,OD,OC,ON,OB为始边的所有角的和为980°,求∠AOB的度数. 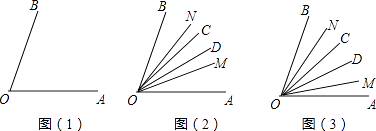
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC. 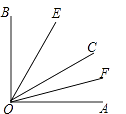
(1)若∠AOB=90°,∠AOC=40°,求∠EOF的度数;
(2)若∠AOB=a,求∠EOF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com