
分析 (1)根据有理数的加减法可以解答本题;
(2)根据有理数的乘方和有理数的加减法可以解答本题;
(3)先把除法转化为乘法,再根据有理数的乘法分配律可以解答本题;
(4)根据有理数的乘方、有理数的乘法和加减法可以解答本题.
解答 解:(1)(-20)+(+3)-(-5)-(+7)
=(-20)+3+5+(-7)
=-19;
(2)(-2)2-22+($\frac{2}{3}$)2-$\frac{2}{{3}^{2}}$
=4-4+$\frac{4}{9}-\frac{2}{9}$
=$\frac{2}{9}$;
(3)(2$\frac{1}{4}$-4$\frac{1}{2}$-1$\frac{1}{8}$)÷(-1$\frac{1}{8}$)
=(2$\frac{1}{4}$-4$\frac{1}{2}$-1$\frac{1}{8}$)×(-$\frac{8}{9}$)
=$\frac{9}{4}×(-\frac{8}{9})$-$\frac{9}{2}×(-\frac{8}{9})-\frac{9}{8}×(-\frac{8}{9})$
=(-2)+4+1
=3;
(4)-14-(1-0.5)×$\frac{1}{3}$-[2-(-3)2]
=-1-$\frac{1}{2}×\frac{1}{3}-[2-9]$
=-1-$\frac{1}{6}-(-7)$
=$-1-\frac{1}{6}+7$
=$5\frac{5}{6}$.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
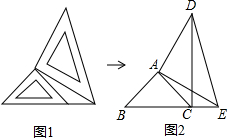 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,点B、C、E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,点B、C、E在同一条直线上,连结DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com