练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠C=90°，∠A=30°，边AB的垂直平分线DE交AC于D，若CD=10cm，则AD=____________ cm

    【答案】20

    【解析】

    根据题意得出∠ABC=60°，再根据线段的垂直平分线的性质得到DA=DB，得出∠ABD=∠A=30°，从而求出∠DBC=30°,根据直角三角形中，30°所对的直角边是斜边的一半求出BD的长即可得出答案．

    解：在△ABC中，∠C=90°，∠A=30°，

    ∴∠ABC=60°

    ∵DE是边AB的垂直平分线，
    ∴DA=DB，
    ∴∠ABD=∠A=30°，

    ∴∠DBC=∠ABC -∠ABD =30°

    在RtCBD中，CD=10cm，
    ∴DB=2CD=20cm，
    ∴DA=20cm

    故答案为：20．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为改善南宁市的交通现状，市政府决定修建地铁，甲、乙两工程队承包地铁1号线的某段修建工作，从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的3倍；若由甲队先做20天，剩下的工程再由甲、乙两队合作10天完成．

    求甲、乙两队单独完成这项工程各需多少天？

    已知甲队每天的施工费用为万元，乙队每天的施工费用为万元，工程预算的施工费用为500万元，为缩短工期，拟安排甲、乙两队同时开工合作完成这项工程，那么工程预算的施工费用是否够用？若不够用，需增加多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

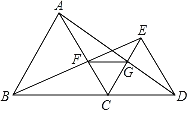
    【题目】如图，B、C、D在同一直线上，△ABC和△CDE都是等边三角形，且在直线BD的同侧，连接BE交AC于点F，连接AD交CE于点G，连接FG．

    （1）求证：AD＝BE；

    （2）求证：△ACG≌△BCF；

    （3）试猜想△CFG的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销，商场又用68000元购进第二批这种运动服，所购数量是第一批购进数量的2倍，但每套进价多了10元．

    （1）该商场两次共购进这种运动服多少套？

    （2）如果这两批运动服每套的售价相同，且全部售完后总利润不低于20%，那么每套售价至少是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

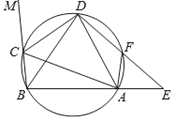
    【题目】如图，在圆内接四边形ABCD中，CD为△BAC的外角平分线，F为弧AD上一点，BC=AF，延长DF与BA的延长线交于E．

    （1）求证：AD=BD；

    （2）若AC=10，AF=3，DF：FE=3：2，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

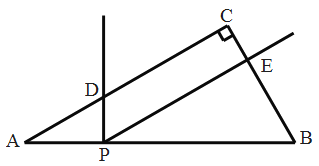
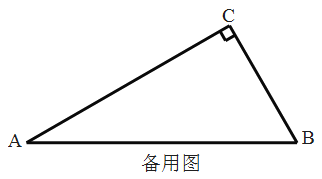
    【题目】如图，在△ABC中，∠ACB=90°，∠A=30°，AB=4，点P是AB边上的一个动点。过点P作AB的垂线交AC边于点D，以PD为边作∠DPE=60°，PE交BC边于点E。

    （1）以点D为AC边的中点时，求BE的长

    （2）当PD=PE时，求AP的长；

    （3）设AP的长为x，四边形CDPE的面积为y，求出y与x的函数解析式及自变量的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线与轴交于点、与轴交于点，直线与轴交于点，将直线沿直线翻折，点恰好落在轴上的点，则直线对应的函数关系式为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

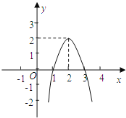
    【题目】二次函数的图象如图所示，根据图象回答：

    当时，写出自变量的值．

    当时，写出自变量的取值范围．

    写出随的增大而减小的自变量的取值范围．

    若方程有两个不相等的实数根，求的取值范围（用含、、的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC是△ABC和△ADC的公共边，下列条件中不能判定△ABC≌△ADC的是（ ）

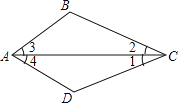
    A．AB=AD，∠2=∠1

    B．AB=AD，∠3=∠4

    C．∠2=∠1，∠3=∠4

    D．∠2=∠1，∠B=∠D

    查看答案和解析>>

    同步练习册答案