
【题目】如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() )
)
(1)求m的取值范围;
(2)若OA=3OB,求抛物线的解析式;
(3)在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.
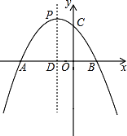
【答案】(1)m>﹣1;(2)y=﹣x2﹣2x+3;(3)存在点Q(﹣1,2)使得△BQC的周长最短.
【解析】
(1)将抛物线的问题转化到一元二次方程中,利用一元二次方程根的判别式和根与系数的关系解决;
(2)先用一元二次方程的两根表示出OA,OB,再用根与系数的关系即可;
(3)先由于点A,B关于抛物线的对称轴PD对称,连接AC与PD的交点就是使△BQC的周长最短,然后确定出直线AC解析式,最后将抛物线的对称轴代入直线AC解析式中即可.
(1)令y=0,则有﹣x2﹣2x+m+1=0,
即:x1 , x2是一元二次方程x2+2x﹣(m+1)=0,
∵抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,
∴x1x2=﹣(m+1),x1+x2=﹣2,
△=4+4(m+1)>0,
∴m>﹣2
∵x1<0,x2>0,
∴x1x2<0,
∴﹣(m+1)<0,
∴m>﹣1,
即m>﹣1
(2)解:∵A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,
∴OA=﹣x1 , OB=x2 ,
∵OA=3OB,
∴﹣x1=3x2 , ①
由(1)知,x1+x2=﹣2,②
x1x2=﹣(m+1),③
联立①②③得,x1=﹣3,x2=1,m=2,
∴抛物线的解析式y=﹣x2﹣2x+3
(3)存在点Q,
理由:如图,
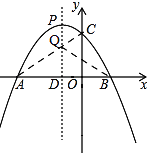
连接AC交PD于Q,点Q就是使得△BQC的周长最短,(∵点A,B关于抛物线的对称轴PD对称,)
连接BQ,
由(2)知,抛物线的解析式y=﹣x2﹣2x+3;x1=﹣3,
∴抛物线的对称轴PD为x=﹣1,C(0,3),A(﹣3,0),
∴用待定系数法得出,直线AC解析式为y=x+3,
当x=﹣1时,y=2,
∴Q(﹣1,2),
∴点Q(﹣1,2)使得△BQC的周长最短


科目:初中数学 来源: 题型:
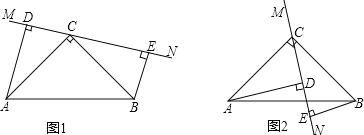
【题目】△ABC中,![]() ∠ACB=900,AC=BC,直线MN经过点C,且
∠ACB=900,AC=BC,直线MN经过点C,且![]() AD⊥MN于D,
AD⊥MN于D,![]() BE⊥MN于E.
BE⊥MN于E.
![]() 当直线MN绕点C旋转到图1的位置时,求证:
当直线MN绕点C旋转到图1的位置时,求证: ![]() ≌△CBE;②DE=AD+BE;
≌△CBE;②DE=AD+BE;
![]() 当直线MN绕点C旋转到图2的位置时,
当直线MN绕点C旋转到图2的位置时,![]() 中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.5 | 9.5 | 9.6 | 9.6 |
方差/环2 | 5.1 | 4.7 | 4.5 | 5.1 |
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用对称性可设计出美丽的图案.在边长为1的方格纸中,有如图所示的四边形(顶点都在格点上).
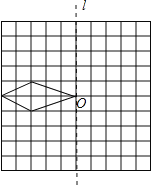
(1)先作出该四边形关于直线![]() 成轴对称的图形,再作出你所作的图形连同原四边形绕0点按顺时针方向旋转90o后的图形;
成轴对称的图形,再作出你所作的图形连同原四边形绕0点按顺时针方向旋转90o后的图形;
(2)完成上述设计后,整个图案的面积等于_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
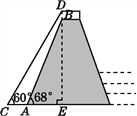
【题目】我国南水北调中线工程的起点是丹江口水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位,如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡底端水平方向增加的宽度AC.(结果精确到0.1米,参考数据:sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.5,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
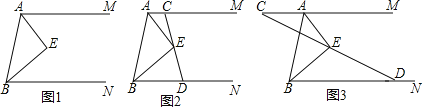
(1)求![]() 的度数;
的度数;
(2)如图2,过点![]() 的直线交射线
的直线交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,过点![]() 的直线交射线
的直线交射线![]() 的反向延长线于点
的反向延长线于点![]() ,交射线
,交射线![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com