
分析 (1)先移项得到)|3x-1|=5,利用绝对值的意义得到3x-1=5或3x-1=-5,然后分别解两个一次方程;
(2)利用绝对值的意义讨论:当b+1<0或b+1=0或b+1>0时确定方程的解的个数,
解答 解:(1)|3x-1|=5,
3x-1=5或3x-1=-5,
所以x=2或x=-$\frac{4}{3}$;
(2)∵|x-2|≥0,
∴当b+1<0,即b<-1时,方程无解;
当b+1=0,即b=-1时,方程只有一个解;
当b+1>0,即b>-1时,方程有两个解.
点评 本题考查了含绝对值符号的一元一次方程:解含绝对值符号的一元一次方程要根据绝对值的性质和绝对值符号内代数式的值分情况讨论,即去掉绝对值符号得到一般形式的一元一次方程,再求解.


科目:初中数学 来源: 题型:选择题
| 工序 时间 模型 | 打磨(A组) | 组装(B组) |
| 模型甲 | 9分钟 | 5分钟 |
| 模型乙 | 6分钟 | 11分钟 |
| A. | 20分钟 | B. | 22分钟 | C. | 26分钟 | D. | 31分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<-1 | B. | a≠0 | C. | a<1且a≠0 | D. | a<-1或a≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
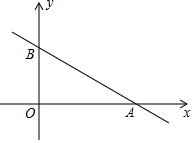 如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.
如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com