
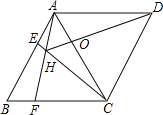
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【答案】D.
【解析】
试题分析:∵四边形ABCD是菱形,
∴AB=BC,
∵AB=AC,
∴AB=BC=AC,
即△ABC是等边三角形,
同理:△ADC是等边三角形
∴∠B=∠EAC=60°,
在△ABF和△CAE中,
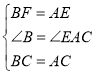 ,
,
∴△ABF≌△CAE(SAS);
故①正确;
∴∠BAF=∠ACE,
∵∠AEH=∠B+∠BCE,
∴∠AHC=∠BAF+∠AEH=∠BAF+∠B+∠BCE=∠B+∠ACE+∠BCE=∠B+∠ACB=60°+60°=120°
故②正确;
∵∠BAF=∠ACE,∠AEC=∠AEC,
∴△AEH∽△CEA,
故③正确;
在菱形ABCD中,AD=AB,
∵△AEH∽△CEA,∴△ABF≌△CAE,
∴△AEH∽△ABF,
∴![]() ,
,
∴![]() ,
,
∴AEAD=AHAF,
故④正确,
故选D.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个.

A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为(![]() ,
,![]() ).
).
[运用]
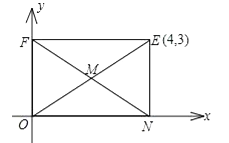
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 如图
如图![]() ,直线
,直线![]() 的经过点
的经过点![]() 和点
和点![]() .
.
![]() 求m、n的值;
求m、n的值;
![]() 如果抛物线
如果抛物线![]() 经过点A、B,该抛物线的顶点为点P,求
经过点A、B,该抛物线的顶点为点P,求![]() 的值;
的值;
![]() 设点Q在直线
设点Q在直线![]() 上,且在第一象限内,直线
上,且在第一象限内,直线![]() 与y轴的交点为点D,如果
与y轴的交点为点D,如果![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .过点
.过点![]() 的直线
的直线![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .易证:
.易证:![]() (不需要证明).
(不需要证明).
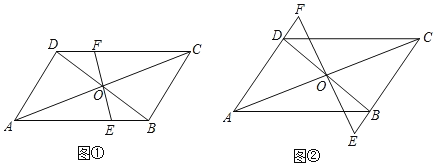
探究:若图①中的直线![]() 分别交边
分别交边![]() 、
、![]() 的延长线于点
的延长线于点![]() 、
、![]() ,其它条件不变,如图②.
,其它条件不变,如图②.
求证:![]() .
.
应用:在图②中,连结![]() .若
.若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的长是__________,四边形
的长是__________,四边形![]() 的面积是__________.
的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有线段AB和点C,按下列语句要求画图与填空:
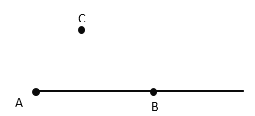
(1)作射线AC;
(2)用尺规在线段AB的延长线上截取BD=AC;
(3)连接BC
(4)有一只蚂蚁想从点A爬到点B,它应该沿路径(填序号)______(①AB,②![]() )爬行最近,这样爬行所运用到的数学原理是_____________________.
)爬行最近,这样爬行所运用到的数学原理是_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段MN是周长为36cm的圆的直径(圆心为O),动点A从点M出发,以![]() 的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为
的速度沿顺时针方向在圆周上运动,经过点N时,其速度变为![]() ,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以
,并以这个速度继续沿顺时针方向运动之点M后停止。在动点A运动的同时,动点B从点N出发,以![]() 的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为
的速度沿逆时针方向在圆周上运动,绕一周后停止运动。设点A、点B运动时间为![]() .
.
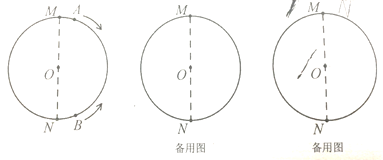
(1)连接OA、OB,当t=4时,![]() = °,在整个运动过程中,当
= °,在整个运动过程中,当![]() 时,点A运动的路程为 cm(第2空结果用含t的式子表示);
时,点A运动的路程为 cm(第2空结果用含t的式子表示);
(2)当A、B两点相遇时,求运动时间t;
(3)连接OA、OB,当![]() 时,请直接写出所有符合条件的运动时间t.
时,请直接写出所有符合条件的运动时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
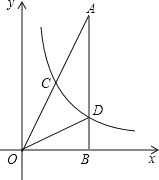
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)求反比例函数解析式;
(2)求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com