
【题目】定义:有三个内角相等的四边形叫三等角四边形.
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
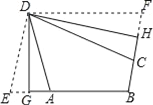
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
科目:初中数学 来源: 题型:
【题目】天气预报说“中山市明天降水概率是20%”,理解正确的是( )
A. 中山市明天将有20%的地区降水
B. 中山市明天降水的可能性较小
C. 中山市明天将有20%的时间降水
D. 中山市明天降水的可能性较大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的顶点坐标是(﹣1,3),与x轴的交点是(2,0),则另一个交点为( )
A. (0,﹣3) B. (﹣3,0) C. (﹣4,0) D. (﹣2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,抛物线![]() 过A、B两点,且与x轴交于另一点C.
过A、B两点,且与x轴交于另一点C.
(1)求b、c的值;
(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;
(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内以点,连接PA、PC、PG,分别以AP、AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR
①求证:PG=RQ;
②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某服装厂现有甲种布料50米,乙种布料27米,现计划用这两种布料生产A,B两种型号的时装共60套. 已知做一套A型号的时装需用甲种布料1米,乙种布料0.2米,可获利30元;做一套B型号的时装需用甲种布料0.5米,乙种布料0.8米,可获利20元. 设生产A型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)之间的函数表达式,并求出自变量的取值范围.
(2)当生产A型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com