Question

10．将一个直角三角形纸片ABO放置在平面直角坐标系中，点$A（\sqrt{3}，0）$，点B（0，1），点O（0，0）．P是边AB上的一点（点P不与点A，B重合），沿着OP折叠该纸片，得点A的对应点A'．
（1）如图①，当点A'在第一象限，且满足A'B⊥OB时，求点A'的坐标；
（2）如图②，当P为AB中点时，求A'B的长；
（3）当∠BPA'=30^°时，求点P的坐标（直接写出结果即可）．

Answer 1

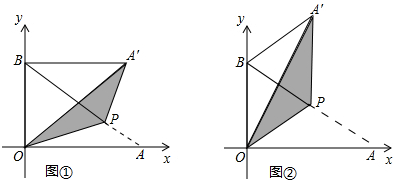
分析 （1）由点A和B的坐标得出OA=$\sqrt{3}$，OB=1，由折叠的性质得：OA'=OA=$\sqrt{3}$，由勾股定理求出A'B=$\sqrt{2}$，即可得出点A'的坐标为（$\sqrt{2}$，1）；
（2）由勾股定理求出AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2，证出OB=OP=BP，得出△BOP是等边三角形，得出∠BOP=∠BPO=60°，求出∠OPA=120°，由折叠的性质得：∠OPA'=∠OPA=120°，PA'=PA=1，证出OB∥PA'，得出四边形OPA'B是平行四边形，即可得出A'B=OP=1；
（3）分两种情况：①点A'在y轴上，由SSS证明△OPA'≌△OPA，得出∠A'OP=∠AOP=$\frac{1}{2}$∠AOB=45°，得出点P在∠AOB的平分线上，由待定系数法求出直线AB的解析式为y=-$\frac{\sqrt{3}}{3}$x+1，即可得出点P的坐标；
②由折叠的性质得：∠A'=∠A=30°，OA'=OA，作出四边形OAPA'是菱形，得出PA=OA=$\sqrt{3}$，作PM⊥OA于M，由直角三角形的性质求出PM=$\frac{1}{2}$PA=$\frac{\sqrt{3}}{2}$，把y=$\frac{\sqrt{3}}{2}$代入y=-$\frac{\sqrt{3}}{3}$x+1求出点P的纵坐标即可．

解答 解：（1）∵点$A（\sqrt{3}，0）$，点B（0，1），
∴OA=$\sqrt{3}$，OB=1，
由折叠的性质得：OA'=OA=$\sqrt{3}$，
∵A'B⊥OB，
∴∠A'BO=90°，
在Rt△A'OB中，A'B=$\sqrt{OA{'}^{2}-O{B}^{2}}$=$\sqrt{2}$，
∴点A'的坐标为（$\sqrt{2}$，1）；

（2）在Rt△ABO中，OA=$\sqrt{3}$，OB=1，
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2，
∵P是AB的中点，
∴AP=BP=1，OP=$\frac{1}{2}$AB=1，
∴OB=OP=BP
∴△BOP是等边三角形，
∴∠BOP=∠BPO=60°，
∴∠OPA=180°-∠BPO=120°，
由折叠的性质得：∠OPA'=∠OPA=120°，PA'=PA=1，
∴∠BOP+∠OPA'=180°，
∴OB∥PA'，
又∵OB=PA'=1，
∴四边形OPA'B是平行四边形，
∴A'B=OP=1；

（3）设P（x，y），分两种情况：
①如图③所示：点A'在y轴上，
在△OPA'和△OPA中，$\left\{\begin{array}{l}{OA'=OA}&{\;}\\{PA'=PA}&{\;}\\{OP=OP}&{\;}\end{array}\right.$，
∴△OPA'≌△OPA（SSS），
∴∠A'OP=∠AOP=$\frac{1}{2}$∠AOB=45°，
∴点P在∠AOB的平分线上，
设直线AB的解析式为y=kx+b，
把点$A（\sqrt{3}，0）$，点B（0，1）代入得：$\left\{\begin{array}{l}{\sqrt{3}k+b=0}\\{b=1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=1}\end{array}\right.$，
∴直线AB的解析式为y=-$\frac{\sqrt{3}}{3}$x+1，
∵P（x，y），
∴x=-$\frac{\sqrt{3}}{3}$x+1，
解得：x=$\frac{3-\sqrt{3}}{2}$，
∴P（$\frac{3-\sqrt{3}}{2}$，$\frac{3-\sqrt{3}}{2}$）；
②如图④所示：
由折叠的性质得：∠A'=∠A=30°，OA'=OA，
∵∠BPA'=30°，
∴∠A'=∠A=∠BPA'，
∴OA'∥AP，PA'∥OA，
∴四边形OAPA'是菱形，
∴PA=OA=$\sqrt{3}$，作PM⊥OA于M，如图④所示：
∵∠A=30°，
∴PM=$\frac{1}{2}$PA=$\frac{\sqrt{3}}{2}$，
把y=$\frac{\sqrt{3}}{2}$代入y=-$\frac{\sqrt{3}}{3}$x+1得：$\frac{\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{3}$x+1，
解得：x=$\frac{2\sqrt{3}-3}{2}$，
∴P（$\frac{2\sqrt{3}-3}{2}$，$\frac{\sqrt{3}}{2}$）；
综上所述：当∠BPA'=30^°时，点P的坐标为（$\frac{3-\sqrt{3}}{2}$，$\frac{3-\sqrt{3}}{2}$）或（$\frac{2\sqrt{3}-3}{2}$，$\frac{\sqrt{3}}{2}$）．

点评 本题是几何变换综合题目，考查了折叠的性质、坐标与图形性质、勾股定理、平行四边形的判定与性质、全等三角形的判定与性质、角平分线的性质、直角三角形的性质、待定系数法求直线的解析式、菱形的判定与性质等知识；本题综合性强，难度较大．