
在Rt△ABC中,AC=BC,∠ACB=90°,D是AC的中点,DG⊥AC交AB于点G.
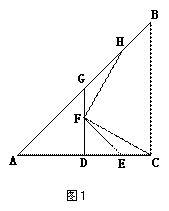
(1)如图1,E为线段DC上任意一点,点F在线段DG上,且DE=DF,连结EF与 CF,过点F作FH⊥FC,交直线AB于点H.
①求证:DG=DC
②判断FH与FC的数量关系并加以证明.
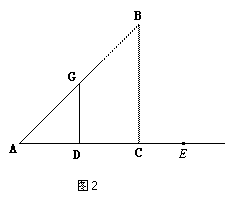
(2)若E为线段DC的延长线上任意一点,点F在射线DG上,(1)中的其他条件不变,借助图2画出图形。在你所画图形中找出一对全等三角形,并判断你在(1)中得出的结论是否发生改变,(本小题直接写出结论,不必证明).
 | |||
 | |||
证明:(1)①∵AC=BC,∠ACB=900
∴∠A=∠B=450
又GD⊥AC
∴∠ADG=900
 在△ADG中,
在△ADG中,
∠A+∠ADG+∠AGD=1800
∴∠AGD=450
∴∠A=∠AGD
∴AD=DG
又D是AC中点
∴AD=DC
∴DG=DC
②由①DG=DC
又∵DF=DE
∴DF-DG=DC-DE
即FG=CE .
由①∠AGD=450
∴∠HGF=1800-450=1350
又DE=DF,∠EDF=900
∴∠DEF=450
∴∠CEF=1800-450=1350
∴∠HGF=∠FEC
又HF⊥CF
∴∠HFC=900
∴∠GFH+∠DFC=1800-900=900
又Rt△FDC中
 ∠DFC+∠ECF=900
∠DFC+∠ECF=900
∴∠GFH=∠ECF
在△FGH和△CEF中
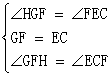
∴△FGH≌△CEF(ASA)
∴FH=FC
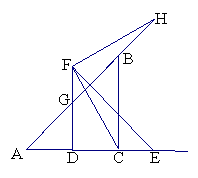
(2)图略(10分)
△FHG≌△CFE
不变,FH=FC


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com