练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．某几何体的三视图及相关数据如图所示．

    （1）说出该几何体的名称和它的高；
    （2）求该几何体的全面积S．

    分析 （1）由几何体的主视图和左视图，俯视图是圆，可以判断这个几何体是圆锥；
    （2）根据S=圆锥侧面积+圆锥底面积即可得到结论．

    解答 解：（1）圆锥，b；
    （2）S=圆锥侧面积+圆锥底面积=$\frac{1}{2}$×2πa-c+πa2=πac+πa2
    =πa（c+a）．

    点评 此题主要考查了三视图的知识和圆锥侧面面积的计算；解决此类图的关键是由三视图得到立体图形；学生由于空间想象能力不够，找不到圆锥的底面半径，或者对圆锥的侧面面积公式运用不熟练，易造成错误．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

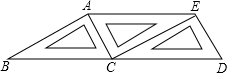    8．如图，将三个相同的三角尺不重叠不留空隙地拼在一起，观察图形，在线段AB、AC、AE、ED、EC、DB中，相互平行的线段有（　　）
    A．1组B．2组C．3组D．4组

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

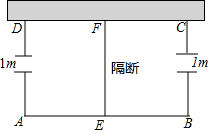    9．如图所示，利用一面墙（墙的长度足够），用篱笆围成一个形如矩形ABCD的场地，在AD，BC边上各有一个宽为1m的缺口，在场地中有用篱笆做的隔断EF，且EF⊥AB，AB＞EF，已知所用篱笆总长度为38m．
    （1）设隔断EF的长为x（m），请用含x的代数式表示AB的长．
    （2）所围成形如矩形ABCD的场地的面积为100m2时，求AB的长．
    （3）所围成矩形ABCD场地的面积能否为140m2？若能，求AB的长；若不能，说明理由．并写出所围成的矩形ABCD场地面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在平面直角坐标系中，A（-3，1）B（2，4），在x轴上求一点C使得CA+CB最小，则C点坐标为（-2，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

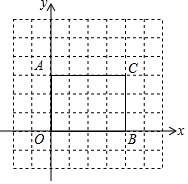    13．如图所示，矩形AOBC各点的坐标分别为A（0，3），O（0，0），B（4，0），C（4，3）．以原点O为位似中心，将这个矩形缩小为原来的$\frac{1}{2}$，写出新矩形A′O′B′C′各顶点的坐标并画出图形（只要画出一个）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解方程：
    （1）5x=3（x-6）；
    （2）3x+$\frac{x-1}{2}$=3-$\frac{2x-1}{3}$；
    （3）$\frac{3}{4}[\frac{4}{3}（\frac{1}{4}x-1）+8]=\frac{7}{3}+\frac{2}{3}x$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列命题中的假命题是（　　）
    A．同位角一定相等B．平移不改变图形的形状和大小
    C．无理数是无限不循环小数D．点M（a，-a）可能在第二象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

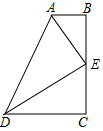    7．如图，四边形ABCD中，AB∥CD，∠B=∠C=90°，E是BC边上的中点，AE平分∠DAB，∠ADE=30°，下面有五个结论：
    ①DE平分∠ADC；②AB+CD=AD；③S四边形ABCD=2S△ADE；④△ADE不是直角三角形；⑤AD=2AE，其中正确结论的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．为奖励在演讲比赛中获奖的同学，大队辅导员王老师负责为获奖同学买奖品，要求每人一件．王老师到文具店看了商品后，决定在钢笔和笔记本中选择．如果买3个笔记本和2支钢笔，则需84元；如果买4个笔记本和3支钢笔，则需118元．
    （1）求笔记本和钢笔的单价分别为多少元？
    （2）售货员提示，买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受7.5折优惠，
    ①若买x（x＞0）支钢笔需要花y1元，请你用含x的式子表示y1；
    ②王老师决定买同一种奖品，并且数量超过10个，请你帮王老师判断买哪种奖品更省钱．

    查看答案和解析>>

    同步练习册答案