
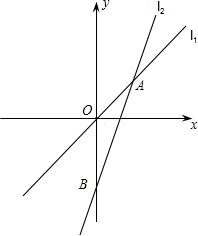
 如图,在平面直角坐标系中,直线l1:y=$\frac{4}{3}$x与直线l2:y=kx+b相交于点A,点A的横坐标为3,直线l2交y轴于点B,且OA=$\frac{1}{2}$OB.
如图,在平面直角坐标系中,直线l1:y=$\frac{4}{3}$x与直线l2:y=kx+b相交于点A,点A的横坐标为3,直线l2交y轴于点B,且OA=$\frac{1}{2}$OB.分析 (1)把点A的横坐标代入进行解答即可;
(2)根据直线的平移特点进行解答即可.
解答 解:(1)根据题意,点A的横坐标为3,代入直线l1:$y=\frac{4}{3}x$中,
得点A的纵坐标为4,即点A(3,4);
即OA=5,又|OA|=$\frac{1}{2}$|OB|.
即OB=10,且点B位于y轴上,
即得B(0,-10);
将A、B两点坐标代入直线l2中,得4=3k+b;
-10=b;
解之得,k=$\frac{14}{3}$,b=-10;
即直线l2的解析式为y=$\frac{14}{3}$x-10;
(2)根据题意,平移后的直线l1的直线方程为$y=\frac{4}{3}(x+3)=\frac{4}{3}x+4$;
即点C的坐标为(0,4);
联立线l2的直线方程,解得x=$\frac{21}{5}$,y=$\frac{28}{5}$,
即点D($\frac{21}{5}$,$\frac{28}{5}$);
又点B(0,-10),如图所示:
故△BCD的面积S=$\frac{1}{2}×\frac{21}{5}×14=\frac{147}{5}$.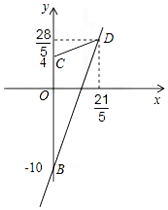
点评 此题考查一次函数与几何变换问题,关键是根据直线的平移特点进行解答.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,二次函数y=ax2+bx+6的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、B两点的横坐标分别为1和3.
如图,在平面直角坐标系中,二次函数y=ax2+bx+6的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、B两点的横坐标分别为1和3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )| A. | cosC=$\frac{CD}{AC}$ | B. | cosC=$\frac{AC}{BC}$ | C. | cosC=$\frac{AD}{AC}$ | D. | cosC=$\frac{AD}{AB}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
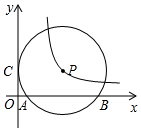 如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).双曲线y=$\frac{k}{x}$恰好经过圆心P,那么k的值是15.
如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).双曲线y=$\frac{k}{x}$恰好经过圆心P,那么k的值是15.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
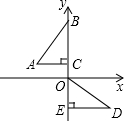 如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| B. | △ABC绕点C逆时针旋转90°,再向下平移3 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C顺时针旋转90°,再向下平移3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
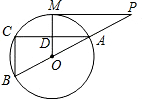 如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.
如图,MP切⊙O于点M,直线PO交⊙O于点A、B,弦AC∥MP,交OM于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com