
分析 (1)首先求出每组中两个数的值各是多少,然后根据有理数大小比较的方法,比较出每组中两个数的大小即可.
(2)从第(1)题的结果经过归纳,猜想nn+1和(n+1)n的大小关系即可.
(3)根据归纳猜想得到的一般结论,比较出20132014与20142013的两个数的大小即可.
解答 解:(1)①12=1,21=2,
∵1<2,
∴12<21.
②23=8,32=9,
∵8<9,
∴23<32.
③34=81,43=64,
∵81>64,
∴34>43.
④45=1024,54=625,
∵1024>625,
∴45>54.
⑤56=15625,65=7776,
∵15625>7776,
∴56>65.
(2)从第(1)题的结果经过归纳,可以猜想nn+1和(n+1)n的大小关系是$\left\{\begin{array}{l}{{n}^{n+1}{<(n+1)}^{n}(n=1,2)}\\{{n}^{n+1}{>(n+1)}^{n}(n≥3)}\end{array}\right.$.
(3)∵2013<2014,
∴20132014>20142013.
故答案为:<、<、>、>、>、$\left\{\begin{array}{l}{{n}^{n+1}{<(n+1)}^{n}(n=1,2)}\\{{n}^{n+1}{>(n+1)}^{n}(n≥3)}\end{array}\right.$.
点评 此题主要考查了有理数大小比较的方法,以及探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法.


科目:初中数学 来源: 题型:解答题
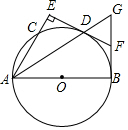 如图△ABG中,∠ABG=90°,以AB为直径作⊙O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.
如图△ABG中,∠ABG=90°,以AB为直径作⊙O交于D点,D是弧BC的中点,过D作AC的垂线,垂足为E,ED的延长线交BG于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
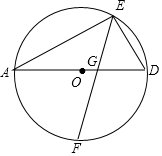 以AD为直径作⊙O,F是半圆弧$\widehat{AD}$上中点,E是半圆弧$\widehat{AD}$上一点,EA=8,ED=6,连接EF交AD于点G,求tan∠AGF的值.
以AD为直径作⊙O,F是半圆弧$\widehat{AD}$上中点,E是半圆弧$\widehat{AD}$上一点,EA=8,ED=6,连接EF交AD于点G,求tan∠AGF的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
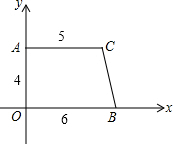 如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,
如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
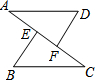 如图,在△AFD和△CEB中,点A、E、F、C在同一条直线上,有下列四个判断:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.请以其中三个为已知条件,剩下一个作为结论,编一道数学题(用序号???⇒?的形式写出),并写出证明过程.
如图,在△AFD和△CEB中,点A、E、F、C在同一条直线上,有下列四个判断:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.请以其中三个为已知条件,剩下一个作为结论,编一道数学题(用序号???⇒?的形式写出),并写出证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6,3$\sqrt{2}$ | B. | 6,3 | C. | 3$\sqrt{2}$,3 | D. | 6$\sqrt{2}$,3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com