
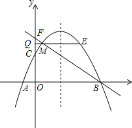
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
(1)求抛物线的解析式,并写出其顶点坐标;
(2)当S△MFQ:S△MEB=1:3时,求点M的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2,顶点坐标为(
x+2,顶点坐标为(![]() ,
,![]() );(2)(1,3)或(﹣12,﹣88).
);(2)(1,3)或(﹣12,﹣88).
【解析】
试题分析:(1)把点A、B、C的坐标代入抛物线解析式得到关于a、b、c的三元一次方程组,然后求解即可,再把函数解析式整理成顶点式形式,然后写出顶点坐标;
(2)根据点M的坐标表示出点Q、E的坐标,再设直线BM的解析式为y=kx+b(k≠0),然后利用待定系数法求出一次函数解析式,再求出点F的坐标,然后求出MQ、FQ、ME,再表示出△MFQ和△MEB的面积,然后列出方程并根据m的取值范围整理并求解得到m的值,再根据点M在抛物线上求出n的值,然后写出点M的坐标即可.
试题解析:(1)∵抛物线y=ax2+bx+c过点A(﹣1,0),B(4,0),C(0,2),
∴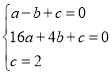 ,
,
解得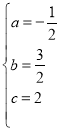 ,
,
∴y=﹣![]() x2+
x2+![]() x+2,
x+2,
∵y=﹣![]() x2+
x2+![]() x+2=﹣
x+2=﹣![]() (x2﹣3x+
(x2﹣3x+![]() )+
)+![]() +2=﹣
+2=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴顶点坐标为(![]() ,
,![]() );
);
(2)∵M(m,n),
∴Q(0,n),E(3﹣m,n),
设直线BM的解析式为y=kx+b(k≠0),
把B(4,0),M(m,n)代入得![]() ,
,
解得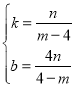 ,
,
∴![]() ,
,
令x=0,则y=![]() ,
,
∴点F的坐标为(0,![]() ),
),
∴MQ=|m|,FQ=|![]() ﹣n|=|
﹣n|=|![]() |,ME=|3﹣m﹣m|=|3﹣2m|,
|,ME=|3﹣m﹣m|=|3﹣2m|,
∴S△MFQ=![]() MQFQ=
MQFQ=![]() |m||
|m||![]() |=
|=![]() |
|![]() |,
|,
S△MEB=![]() ME|n|=
ME|n|=![]() |3﹣2m||n|,
|3﹣2m||n|,
∵S△MFQ:S△MEB=1:3,
∴![]() |
|![]() |×3=
|×3=![]() |3﹣2m||n|,
|3﹣2m||n|,
即|![]() |=|3﹣2m|,
|=|3﹣2m|,
∵点M(m,n)在对称轴左侧,
∴m<![]() ,
,
∴![]() =3﹣2m,
=3﹣2m,
整理得,m2+11m﹣12=0,
解得m1=1,m2=﹣12,
当m1=1时,n1=﹣![]() ×12+
×12+![]() ×1+2=3,
×1+2=3,
当m2=﹣12时,n2=﹣![]() ×(﹣12)2+
×(﹣12)2+![]() ×(﹣12)+2=﹣88,
×(﹣12)+2=﹣88,
∴点M的坐标为(1,3)或(﹣12,﹣88).


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
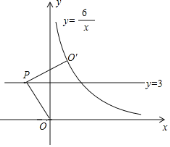
【题目】如图,点P是直线y=3上的动点,连接PO并将PO绕P点旋转90°到PO′,当点O′刚好落在双曲线![]() (x>0)上时,点P的横坐标所有可能值为_____.
(x>0)上时,点P的横坐标所有可能值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() .反比例函数
.反比例函数![]() 在第一象限内的图像经过点
在第一象限内的图像经过点![]() ,交
,交![]() 于点
于点![]() ,
,![]() .
.
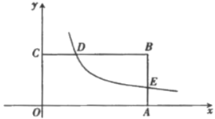
(1)求这个反比例函数的表达式,
(2)动点![]() 在矩形
在矩形![]() 内,且满足
内,且满足![]() .
.
①若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标,
的坐标,
②若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,求点
为顶点的四边形是菱形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
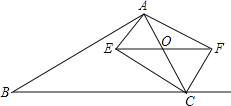
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.
(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形ABCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0②当-1≤x≤3时,y<0③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2④9a+3b+c=0其中正确的是( )
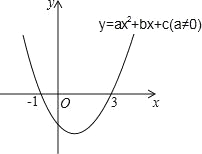
A.①②④ B.①④ C.①②③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠AFC,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°—∠ABD;④∠BDC=![]() ∠BAC,其中正确的结论有_____________。
∠BAC,其中正确的结论有_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在线段
在线段![]() 上,
上,![]() 是线段
是线段![]() 的中点.
的中点.
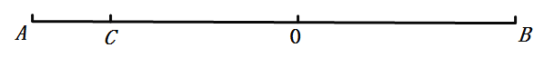
(1)在线段![]() 上,求作点
上,求作点![]() ,使
,使![]() .
.
(要求:尺规作图,不写作法保留作图痕迹)
(2)在(1)的条件下,![]() ,
,
①若![]() ,求
,求![]() 的长;
的长;
②若点![]() 在线段
在线段![]() 上,且
上,且![]() ,请你判断点
,请你判断点![]() 是哪条线段的中点,并说明理由.
是哪条线段的中点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com