
如图所示,平面直角坐标系中,△ABC为等边三角形,其中点A、B、C的坐标分别为(-3,-1)、(-3,-3)、(-3+![]() ,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
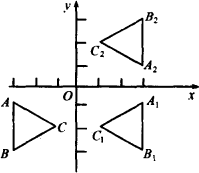
(1)直接写出点C1、C2的坐标;
(2)能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定的回答,并直接写出所旋转的度数;你若认为不能,请作出否定的回答(不必说明理由);
(3)设当△ABC的位置发生变化时,△A2B2C2、△A1B1C1与△ABC之间的对称关系始终保持不变.①当△ABC向上平移多少个单位时,△A1B1C1与△A2B2C2完全重合?并直接写出此时点C的坐标;②将△ABC绕点A顺时针旋转α°(0≤α≤180),使△A1B1C1与△A2B2C2完全重合,此时α的值为多少?点C的坐标又是什么?
|
解:(1)点C1、C2的坐标分别为(3- (2)能通过一次旋转将△ABC旋转到△A2B2的位置,所旋转的度数为180° (3)①当△ABC向上平移2个单位时,△A1B1C1与△A2B2C2完全重合,此时点的坐标为(-3+ 解析:本题以图形与变换、图形与坐标、连续两次轴对称变换与中心对称的关系等有关知识以及空间想象能力作为考查对象,通过图形的运动将平移、旋转、坐标等知识有机地结合在一起,并进一步在运动变化中研究图形坐标的变化,设问层层递进,使得不同水平的学生都有机会表达自己对问题的理解. ①根据△A1B1C1与△A2B2C2完全重合,则对应点的横、纵坐标相等,又△A1B1C1与△A2B2C2对应点的纵坐标互为相反数,而C1(0,y1)与C2(0,y2)是对应点,所以y1=y2且y2+y2=0,因此得y1=y2=0;②由△A1B1C1与△A2B2C2完全重合,则C1与C2必重合,而△ABC与△A2B2C2成中心对称,△ABC必须旋转到使点C在x轴上,因此α=180,C(-3- |


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源:同步轻松练习 八年级 数学 上 题型:059
学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如图)
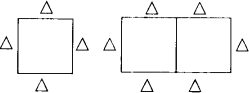
(1)按照这种规定填写下表:
(2)根据表中的数据,将s作为纵坐标,n作为横坐标,在如图所示的平面直角坐标系中找出相应各点.
(3)请你猜一猜上述各点会在某一个函数图象上吗?如果在某一函数图象上,求出该函数的解析式,并利用你探求的结果,求出当n=10时,s的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山西省九年级上学期期末考试数学试卷(解析版) 题型:解答题
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C(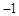 ,0),如图所示:抛物线
,0),如图所示:抛物线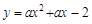 经过点B。
经过点B。

(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:专项题 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com