
如图,A、B两点在函数y= (x>0)的图象上.
(x>0)的图象上.
(1)求m的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数.
(1)m=6 直线AB的解析式为y=﹣x+7 (2)3
解析试题分析:(1)将A点或B点的坐标代入y= 求出m,再将这两点的坐标代入y=kx+b求出k、b的值即可得到这个函数的解析式;
求出m,再将这两点的坐标代入y=kx+b求出k、b的值即可得到这个函数的解析式;
(2)画出网格图帮助解答.
解:(1)由图象可知,函数 (x>0)的图象经过点A(1,6),
(x>0)的图象经过点A(1,6),
可得m=6.
设直线AB的解析式为y=kx+b.
∵A(1,6),B(6,1)两点在函数y=kx+b的图象上,
∴ ,
,
解得 .
.
∴直线AB的解析式为y=﹣x+7;
(2)图中阴影部分(不包括边界)所含格点是(2,4),(3,3),(4,2)共3个.
考点:反比例函数的图象;待定系数法求一次函数解析式.
点评:本题考查了一次函数和反比例函数的图象性质,综合性较强,体现了数形结合的思想.


科目:初中数学 来源: 题型:
| k2 | x |
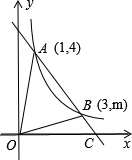 ,4),B(3,m)两点.
,4),B(3,m)两点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
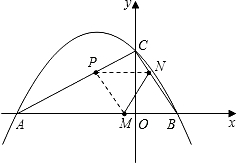 ,Q为项点的三角形与△ABC相似?如果存在,请求出点Q的坐标;如果不存在,请说明理由.
,Q为项点的三角形与△ABC相似?如果存在,请求出点Q的坐标;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
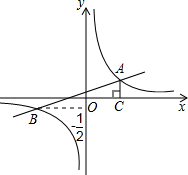 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=| m |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=| m | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com