
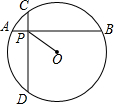
 如图,弦CD⊥AB于P,AB=8,CD=8,⊙O半径为5,则OP长为3$\sqrt{2}$.
如图,弦CD⊥AB于P,AB=8,CD=8,⊙O半径为5,则OP长为3$\sqrt{2}$. 分析 作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,首先利用勾股定理求得OM的长,然后判定四边形OMPN是正方形,求得正方形的对角线的长即可求得OM的长.
解答  解:作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
解:作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
∵AB=CD=8,
∴BM=DN=4,
∴OM=ON=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵AB⊥CD,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
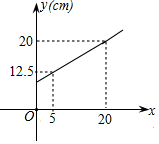 弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是( )
弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是( )| A. | 9cm | B. | 10cm | C. | 10.5cm | D. | 11cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com