练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．世界杯足球赛小组赛规定，每个小组4个队进行单循环比赛，每场比赛胜队得3分，败队得0分，平局时两队各得1分，小组赛完后，总积分最高的2个队出线进入下轮比赛，如果总积分相同，还要按净胜球数排序，一个队要保证出线，这个队至少要积（　　）分．
    A．8B．7C．6D．5

    分析 首先根据题意推出6场比赛后各队的得分之和不超过18分，再分两种情形讨论①若一个队得7分，②若一个队得6分，看看其他队的得分的可能性，即可解决问题．

    解答 解：4个队进行单循环比赛共比赛4×3÷2=6场，每场比赛后两队得分之和或为2分或为2分，所以6场比赛后各队的得分之和不超过18分，
    ①若一个队得7分，剩下的3个队得分之和不超过11分，不可能有两个队得分都大于或等于7分，所以这个队必定出线．
    ②若一个队得6分，则有可能还有两个队均得6分，而净胜球比该队多，该队仍不能出线．
    故选B．

    点评 本题考查了比赛问题中的推理与论证；得到比赛的总场数以及相应的总积分是解决本题的突破点；分类探讨可以出线的小组的最低分是解决本题的难点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

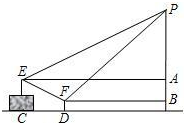    7．广场上有一个充满氢气的气球P，被广告条拽着悬在空中，甲乙二人分别站在E、F处，他们看气球的仰角分别为30°、45°，E点与F点的高度差AB为1米，水平距离CD为5米，FD的高度为0.5米，请问此气球有多高？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知AB是⊙O的直径，BP是⊙O的弦，弦CD⊥AB于点F，交BP于点G，E在CD的延长线上，EP=EG．
    （1）求证：直线EP为⊙O的切线；
    （2）点P在劣弧$\widehat{AC}$上运动，其他条件不变，若BG2=BF•BO，⊙O的半径为3，sinB=$\frac{\sqrt{3}}{3}$，求弦CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．不等式组$\left\{\begin{array}{l}{-3（x+1）-x＜5}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1}\end{array}\right.$的解为（　　）
    A．x＜-2或x≥1B．x＜-2C．-2＜x≤1D．-2$＜x＜\frac{1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

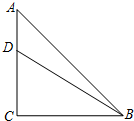    12．如图，在等腰Rt△ABC中，∠C=90°，AC=6，D是AC上一点，若tan∠DBA=$\frac{1}{5}$，则AD的长为（　　）
    A．1B．$\sqrt{3}$C．$\sqrt{2}$D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．AD是△ABC的中线，∠ADC=45°，把△ADC沿直线AD翻折，点C落在点C′的位置，BC=4，则BC′的长为2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如果多项式mx4+（m-2）x3+（2n+1）x3-3x+n不含x3和x2的项，你能求出m，n的值吗？试写出这个多项式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

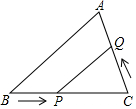    6．如图，在△ABC中，∠C=90°，BC=8cm，4AC-3BC=0，点P从B点出发，沿BC方向以2cm/s的速度移动，点Q从C点出发，沿CA方向以1cm/s的速度移动，若P、Q分别从B、C同时出发，经过多少秒时，△CPQ与△CBA相似？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，在△ABC中，∠ABC=90°，AB=BC，点D是△ABC内部一点，连接AD，BD和CD．
    （1）如图1，若∠BDC=90°，BD=1，CD=2，求AC的长．
    （2）如图2，若CD平分∠ACB，∠BDC=90°，过点B作BE∥AC交AD的延长线于点E，求证：AD=DE．
    （3）如图3，若CD=CB，∠BCD=30°，取线段AC的中点F，连接DF，求证：∠AFD=45°

    查看答案和解析>>

    同步练习册答案