
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠµÄČżµćA£Ø1£¬0£©£¬B£Ø-1£¬0£©£¬P£Ø0£¬-1£©£¬½«Ļ߶ĪABŃŲyÖįĻņÉĻĘ½ŅĘm£Øm£¾0£©øöµ„Ī»³¤¶Č£¬µĆµ½Ļ߶ĪCD£¬¶ž“ĪŗÆŹży=a£Øx-h£©2+kµÄĶ¼Ļó¾¹żµćP”¢C”¢D£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠµÄČżµćA£Ø1£¬0£©£¬B£Ø-1£¬0£©£¬P£Ø0£¬-1£©£¬½«Ļ߶ĪABŃŲyÖįĻņÉĻĘ½ŅĘm£Øm£¾0£©øöµ„Ī»³¤¶Č£¬µĆµ½Ļ߶ĪCD£¬¶ž“ĪŗÆŹży=a£Øx-h£©2+kµÄĶ¼Ļó¾¹żµćP”¢C”¢D£®·ÖĪö £Ø1£©·Ö±š°Ńm=1ŗĶm=2“śČėæɵĆCµÄ×ų±ź£¬øł¾ŻÅ×ĪļĻ߶„µćP£Ø0£¬-1£©Š“³ö½āĪöŹ½ĪŖ£ŗy=ax2-1£¬ŌŁ“śČėC»ņDµÄ×ų±ź¼“æÉ£»
£Ø2£©øł¾ŻĻ߶ĪABŃŲyÖįĻņÉĻĘ½ŅĘm£Øm£¾0£©øöµ„Ī»³¤¶Č£¬µĆµ½Ļ߶ĪCD£¬Š“³öCŗĶDµÄ×ų±ź£¬Ķ¬Ąķ½«CµÄ×ų±ź“śČė½āĪöŹ½ÖŠæÉµĆ½įĀŪ£»
£Ø3£©¢ŁĶ¬ĄķæÉµĆ£ŗa=$\frac{n+1}{2}$£¬ÓÉ£Ø2£©ÖŠµĆ£ŗa=m+1£¬ĮŠµČŹ½æÉµĆ£ŗ
¢Ś·Ö±šŅŌČżøö¶„µćĪŖÖ±½Ē¶„µć£¬Óɹ“¹É¶ØĄķĮŠ·½³ĢæɵĆaµÄÖµ£®
½ā“š ½ā£ŗ£Ø1£©µ±m=1Ź±£¬C£Ø1£¬1£©£¬D£Ø-1£¬1£©£¬
”ßÅ×ĪļĻ߶„µćP£Ø0£¬-1£©£¬
”ąy=ax2-1£¬
°ŃC£Ø1£¬1£©“śČėµĆ£ŗa=2£¬
µ±m=2Ź±£¬C£Ø1£¬2£©£¬D£Ø-1£¬2£©£¬
”ßÅ×ĪļĻ߶„µćP£Ø0£¬-1£©£¬
”ąy=ax2-1£¬
°ŃC£Ø1£¬2£©“śČėµĆ£ŗ2=a-1£¬
a=3£¬
¹Ź“š°øĪŖ£ŗ2£»3£»
£Ø2£©a=m+1£¬ĄķÓÉŹĒ£ŗ
ÓÉĢāŅāµĆ£ŗC£Ø1£¬m£©£¬D£Ø-1£¬m£©
°ŃC£Ø1£¬m£©“śČėÅ×ĪļĻߵĽāĪöŹ½y=ax2-1ÖŠµĆ£ŗm=a-1£¬
”ąa=m+1
£Ø3£©¢ŁÓÉĢāŅāµĆ£ŗC1£Ø1£¬n£©£¬D1£Ø-1£¬n£©£¬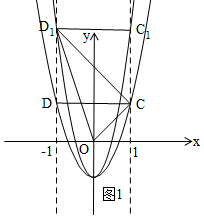
°ŃC1£Ø1£¬n£©“śČėÅ×ĪļĻߵĽāĪöŹ½y=2ax2-1ÖŠµĆ£ŗn=2a-1£¬
”ąa=$\frac{n+1}{2}$£¬
ÓÉ£Ø2£©ÖŖ£ŗa=m+1£¬
”ąm+1=$\frac{n+1}{2}$£¬
”ąn-2m=1£»
¢Ś·ÖČżÖÖĒéæö£ŗ
”ßC£Ø1£¬a-1£©£¬D1£Ø-1£¬2a-1£©£¬O£Ø0£¬0£©£¬
i£©µ±”ĻD1CO=90”揱£¬”÷COD1ŹĒÖ±½ĒČż½ĒŠĪ£¬ČēĶ¼1£¬
Óɹ“¹É¶ØĄķµĆ£ŗ${D}_{1}{C}^{2}+O{C}^{2}={D}_{1}{O}^{2}$£¬
£Ø-1-1£©2+£Ø2a-1-a+1£©2+12+£Øa-1£©2=£Ø-1£©2+£Ø2a-1£©2£¬
a2-a-2=0£¬
£Øa+1£©£Øa-2£©=0£¬
a1=-1£ØÉį£©£¬a2=2£»
ii£©µ±”ĻD1OC=90”揱£¬”÷COD1ŹĒÖ±½ĒČż½ĒŠĪ£¬ČēĶ¼2£¬
Óɹ“¹É¶ØĄķµĆ£ŗ${D}_{1}{O}^{2}+O{C}^{2}={D}_{1}{C}^{2}$£¬
£Ø-1£©2+£Ø2a-1£©2+12+£Øa-1£©2=£Ø1+1£©2+£Øa-1-2a+1£©2£¬
2a2-3a=0£¬
a£Ø2a-3£©=0£¬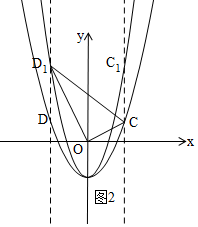
a1=0£ØÉį£©£¬a2=$\frac{3}{2}$£»
iii£©µ±”ĻCD1O=90”ć£¬”÷COD1ŹĒÖ±½ĒČż½ĒŠĪ£¬
Ķ¬ĄķµĆ£ŗ${D}_{1}{C}^{2}+{D}_{1}{O}^{2}=C{O}^{2}$£¬
£Ø-1-1£©2+£Ø2a-1-a+1£©2+£Ø-1£©2+£Ø2a-1£©2=12+£Øa-1£©2£¬
2a2-a+2=0£¬
”÷=1-4”Į2”Į2£¼0£¬
“Ė·½³ĢĪŽŹµŹż½ā£¬
×ŪÉĻĖłŹö£¬µ±”÷COD1ŹĒÖ±½ĒČż½ĒŠĪŹ±£¬aµÄÖµŹĒ$\frac{3}{2}$»ņ2£®
µćĘĄ ±¾ĢāŹĒ¶ž“ĪŗÆŹżµÄ×ŪŗĻĢā£¬æ¼²éĮĖĄūÓĆ“ż¶ØĻµŹż·ØĒ󶞓ĪŗÆŹżµÄ½āĪöŹ½£¬µćµÄĘ½ŅĘ¹ęĀÉ”¢¹“¹É¶ØĄķ£¬²ÉÓĆĮĖ·ÖĄąĢÖĀŪµÄŌŌņ£¬µŚČżĪŹÖŠ£¬µ±Čż½ĒŠĪĪŖÖ±½ĒČż½ĒŠĪŹ±£¬æÉŅŌĄūÓĆ¹“¹É¶ØĄķĮŠ·½³Ģ½ā¾öĪŹĢā£®


 ÓŵČÉśĢāæāĻµĮŠ“š°ø
ÓŵČÉśĢāæāĻµĮŠ“š°ø 53ĢģĢģĮ·ĻµĮŠ“š°ø
53ĢģĢģĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
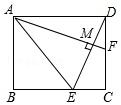 ČēĶ¼ĖłŹ¾£¬ŌŚ¾ŲŠĪABCDÖŠ£¬FŹĒDCÉĻŅ»µć£¬AEĘ½·Ö”ĻBAF½»BCÓŚµćE£¬ĒŅDE”ĶAF£¬“¹×ćĪŖµćM£¬BE=3£¬AE=2$\sqrt{6}$£¬ŌņMFµÄ³¤ŹĒ$\frac{\sqrt{15}}{15}$£®
ČēĶ¼ĖłŹ¾£¬ŌŚ¾ŲŠĪABCDÖŠ£¬FŹĒDCÉĻŅ»µć£¬AEĘ½·Ö”ĻBAF½»BCÓŚµćE£¬ĒŅDE”ĶAF£¬“¹×ćĪŖµćM£¬BE=3£¬AE=2$\sqrt{6}$£¬ŌņMFµÄ³¤ŹĒ$\frac{\sqrt{15}}{15}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŌŚĶųøńÖŠ½ØĮ¢ĮĖĘ½ĆęÖ±½Ē×ų±źĻµ£¬ĆæøöŠ”Õż·½ŠĪµÄ±ß³¤¾łĪŖ1øöµ„Ī»³¤¶Č£¬½«ĖıߊĪABCDČĘ×ų±źŌµćĖ³Ź±Õė·½ĻņŠż×Ŗ180”ćŗóµĆµ½ĖıߊĪA1B1C1D1£®
ČēĶ¼£¬ŌŚĶųøńÖŠ½ØĮ¢ĮĖĘ½ĆęÖ±½Ē×ų±źĻµ£¬ĆæøöŠ”Õż·½ŠĪµÄ±ß³¤¾łĪŖ1øöµ„Ī»³¤¶Č£¬½«ĖıߊĪABCDČĘ×ų±źŌµćĖ³Ź±Õė·½ĻņŠż×Ŗ180”ćŗóµĆµ½ĖıߊĪA1B1C1D1£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
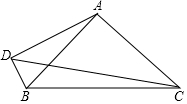 ČēĶ¼£¬¼ŗÖŖ”ĻCAB=90”ć£¬AB=$\frac{\sqrt{2}}{2}$BC£¬AD”ĶBD£¬S”÷ABD=$\frac{3}{40}$BC2£¬sin”ĻCDB=$\frac{\sqrt{2}}{2}$£®
ČēĶ¼£¬¼ŗÖŖ”ĻCAB=90”ć£¬AB=$\frac{\sqrt{2}}{2}$BC£¬AD”ĶBD£¬S”÷ABD=$\frac{3}{40}$BC2£¬sin”ĻCDB=$\frac{\sqrt{2}}{2}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
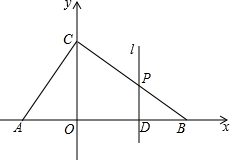 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Rt”÷ABCµÄŠ±±ßABŌŚxÖįÉĻ£¬µćCŌŚyÖįÉĻ£¬”ĻACB=90”ć£¬OC”¢OBµÄ³¤·Ö±šŹĒŅ»ŌŖ¶ž“Ī·½³Ģx2-6x+8=0µÄĮ½øöøł£¬ĒŅOC£¼OB£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Rt”÷ABCµÄŠ±±ßABŌŚxÖįÉĻ£¬µćCŌŚyÖįÉĻ£¬”ĻACB=90”ć£¬OC”¢OBµÄ³¤·Ö±šŹĒŅ»ŌŖ¶ž“Ī·½³Ģx2-6x+8=0µÄĮ½øöøł£¬ĒŅOC£¼OB£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com