
【题目】2019年4月29日至2019年10月7日,2019年中国北京世界园艺博览会(简称北京世园会)在中国北京市延庆区举行,展期162天.这是继云南昆明后第二个获得国际园艺生产者协会批准及国际展览局认证授权举办的A1级国际园艺博览会.北京世园会门票种类分为平日票、指定日票、三次票等票种,同时按销售对象分为普通票、优惠票和团队票(学生享受优惠票,15人以上可以享受团体票).指定日包括开园日、“五一”假期、端午节假期、中秋节假期、“十一”假期这些日期,其余时间为平日;三次票是指除指定日外,同一持票人在展会期间可以任选三天入园的票种. 具体如下表:
平日票价(元/张) | 指定日票价(元/张) | 三次票(元/张) | |
普通票 | 120 | 160 | 300 |
优惠票 | 80 | 100 |
小明,小亮两家共10人打算一起参观北京世园会(10人均需购票).
(1)若他们端午节去北京世园会参观购买门票共用去1360元,问买了普通票和优惠票各几张?
(2)如果他们平日去北京世园会参观,且购买门票的费用不超过2000元,那么在保证游玩的前提下最多可以买几张三次票?共有几种买票方案?分别是什么?
【答案】(1)普通票6张,优惠票4张;(2)最多可以买5张三次票,两种购票方案
【解析】
(1)设需购买普通票x张,优惠票y张,根据小明,小亮两家共10人,购买门票共用去1360元列方程组求解即可;
(2)法1根据题意列出不等式求解;法2根据不考虑三次票的话及全买三次票求出三次票的范围,再讨论即可.
解:(1)设需购买普通票x张,优惠票y张,
依题有![]() ,
,
得![]() ,
,
答:他们需购买普通票6张,优惠票4张;
(2)法1:设他们买了x张三次票,则3<x<7,x为整数,
他们平日去参观世园会,如果不考虑三次票的话,
∵买票需![]() 元,
元,
∴剩下![]() 元,
元,
![]() ,
,
![]() ,
,
![]() ,
,
依题有 ![]() ,
,
得![]() ,
,
又 ![]() x为整数,
x为整数,
![]()
![]() ,
,
答:此时最多可以买5张三次票.
法2:他们平日去参观世园会,如果不考虑三次票的话,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故可以买4张,5张或6张三次票,
讨论:i)若买4张三次票,则![]() ,
,
∴可保证游玩.
ii)若买5张三次票,则
![]() ,
,![]() ,
,
又∵500>440,
∴可保证游玩.
iii)若买6张三次票,则![]() ,
,
∴不可保证游玩.
答:他们最多可以买5张三次票,买5张三次票的前提下共有以下两种购票方案,分别为:三次票5张,普通票1张,优惠票4张;三次票5张,普通票2张,优惠票3张;


科目:初中数学 来源: 题型:
【题目】填空,把下面的推理过程补充完整,并在括号内注明理由:
如图,已知A、B、C、D在同一直线上,AE∥DF,AC=BD,∠E=∠F,求证:BE∥CF.

证明:∵AE∥DF(已知)
∴_________(两直线平行,内错角相等)
∵AC=BD(已知)
又∵AC=AB+BC,BD=BC+CD
∴________(等式的性质)
∵∠E=∠F(已知)
∴△ABE≌△DCF(___________)
∴∠ABE=∠DCF(_________________)
∵ABF+∠CBE=180°,∠DCF+∠BCF=180°
∴∠CBE=∠BCF(__________________)
∴BE∥CF(________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
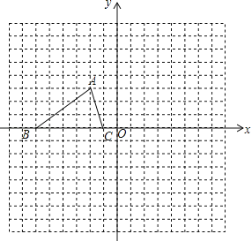
【题目】如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A′的坐标_____;
(2)将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点A″的坐标_____;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的所有可能的坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+4![]() ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+![]() ,其中正确的结论是( )
,其中正确的结论是( )

A. ①②③⑤ B. ①②③④ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,点E在CD上,点F、G在AB上,且AF=FG=BG=DE=CE。以A、B、C、D、E、F、G这7个点中的三个为顶点的三角形中,面积最小的三角形有_________个,面积最大的三角形有__________个。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )

A. 点G B. 点E C. 点D D. 点F
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.
(1)列出原计划种植亩数y(亩)与平均每亩产量x(万斤)之间的函数关系式,并写出自变量x的取值范围;
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:

(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9,
(1)求证:△COD∽△CBE;
(2)求半圆O的半径的长

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com