
 如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,| ɑ | 30° | 40° | 50° | 60° |
| β | 120° | 130° | 140° | 150° |
| γ | 150° | 140° | 130° | 120° |
分析 (1)由圆周角定理即可得出β=α+90°,然后根据D是BC的中点,DE⊥BC,可知∠EDC=90°,由三角形外角的性质即可得出∠CED=α,从而可知O、A、E、B四点共圆,由圆内接四边形的性质可知:∠EBO+∠EAG=180°,即γ=-α+180°;
(2)由(1)及γ=135°可知∠BOA=90°,∠BCE=45°,∠BEC=90°,由于△ABE的面积为△ABC的面积的4倍,所以$\frac{AE}{AC}=4$,根据勾股定理即可求出AE、AC的长度,从而可求出AB的长度,再由勾股定理即可求出⊙O的半径r;
解答 解:(1)猜想:β=α+90°,γ=-α+180°
连接OB,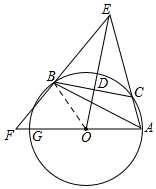
∴由圆周角定理可知:2∠BCA=360°-∠BOA,
∵OB=OA,
∴∠OBA=∠OAB=α,
∴∠BOA=180°-2α,
∴2β=360°-(180°-2α),
∴β=α+90°,
∵D是BC的中点,DE⊥BC,
∴OE是线段BC的垂直平分线,
∴BE=CE,∠BED=∠CED,∠EDC=90°
∵∠BCA=∠EDC+∠CED,
∴β=90°+∠CED,
∴∠CED=α,
∴∠CED=∠OBA=α,
∴O、A、E、B四点共圆,
∴∠EBO+∠EAG=180°,
∴∠EBA+∠OBA+∠EAG=180°,
∴γ+α=180°;
(2)当γ=135°时,此时图形如图所示,
∴α=45°,β=135°,
∴∠BOA=90°,∠BCE=45°,
由(1)可知:O、A、E、B四点共圆,
∴∠BEC=90°,
∵△ABE的面积为△ABC的面积的4倍,
∴$\frac{AE}{AC}=4$,
∴$\frac{CE}{AC}=3$,
设CE=3x,AC=x,
由(1)可知:BC=2CD=6,
∵∠BCE=45°,
∴CE=BE=3x,
∴由勾股定理可知:(3x)2+(3x)2=62,
x=$\sqrt{2}$,
∴BE=CE=3$\sqrt{2}$,AC=$\sqrt{2}$,
∴AE=AC+CE=4$\sqrt{2}$,
在Rt△ABE中,
由勾股定理可知:AB2=(3$\sqrt{2}$)2+(4$\sqrt{2}$)2,
∴AB=5$\sqrt{2}$,
∵∠BAO=45°,
∴∠AOB=90°,
在Rt△AOB中,设半径为r,
由勾股定理可知:AB2=2r2,
∴r=5,
∴⊙O半径的长为5.
点评 本题考查圆的综合问题,涉及圆周角定理,勾股定理,解方程,垂直平分线的性质等知识,综合程度较高,需要学生灵活运用所学知识.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差是21 | B. | 平均数是26 | C. | 众数是22 | D. | 中位数是24 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
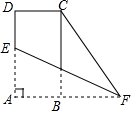 如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )
如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
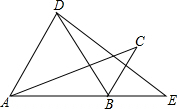 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )| A. | ∠ABD=∠E | B. | ∠CBE=∠C | C. | AD∥BC | D. | AD=BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
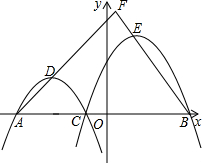 如图,在平面直角坐标系xOy中,已知A,B两点的坐标分别为(-4,0),(4,0),C(m,0)是线段A B上一点(与 A,B点不重合),抛物线L1:y=ax2+b1x+c1(a<0)经过点A,C,顶点为D,抛物线L2:y=ax2+b2x+c2(a<0)经过点C,B,顶点为E,AD,BE的延长线相交于点F.
如图,在平面直角坐标系xOy中,已知A,B两点的坐标分别为(-4,0),(4,0),C(m,0)是线段A B上一点(与 A,B点不重合),抛物线L1:y=ax2+b1x+c1(a<0)经过点A,C,顶点为D,抛物线L2:y=ax2+b2x+c2(a<0)经过点C,B,顶点为E,AD,BE的延长线相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 研发组 | 管理组 | 操作组 | |
| 日工资(元) | 200 | 180 | 160 |
| 人数(人) | 3 | 4 | 5 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省启东市九年级寒假作业测试(开学考试)数学试卷(解析版) 题型:解答题
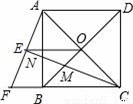
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=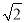 ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com