½ā“š£ŗ½ā£ŗ£Ø1£©ŌŚĮāŠĪABCDÖŠ£¬
”ßAC”ĶBD
”ąAD=
=50£®
”ąĮāŠĪABCDµÄÖܳ¤ĪŖ200£®
£Ø2£©¹żµćM×÷MP”ĶAD£¬“¹×ćĪŖµćP£®
¢Łµ±0£¼t”Ü40Ź±£¬Čē“šĶ¼1£¬
”ßsin”ĻOAD=
=
=
£¬
”ąMP=AM•sin”ĻOAD=
t£®
S=
DN•MP=
”Įt”Į
t=
t
2£»

¢Śµ±40£¼t”Ü50Ź±£¬Čē“šĶ¼2£¬MD=70-t£¬
”ßsin”ĻADO=
=
=
£¬”ąMP=
£Ø70-t£©£®
”ąS
”÷DMN=
DN•MP=
”Įt”Į
£Ø70-t£©=
-t
2+28t=
-£Øt-35£©
2+490£®
”ąS=
| | t2(0£¼t”Ü40) | | -(t-35)2+490(40£¼t”Ü50) |
| |
µ±0£¼t”Ü40Ź±£¬SĖętµÄŌö“ó¶ųŌö“󣬵±t=40Ź±£¬×ī“óÖµĪŖ480£®
µ±40£¼t”Ü50Ź±£¬SĖętµÄŌö“ó¶ų¼õŠ”£¬µ±t=40Ź±£¬×ī“óÖµĪŖ480£®
×ŪÉĻĖłŹö£¬SµÄ×ī“óÖµĪŖ480£®
£Ø3£©“ęŌŚ2øöµćP£¬Ź¹µĆ”ĻDPO=”ĻDON£®
·½·ØŅ»£ŗČē“šĶ¼3ĖłŹ¾£¬¹żµćN×÷NF”ĶODÓŚµćF£¬
ŌņNF=ND•sin”ĻODA=30”Į
=24£¬DF=ND•cos”ĻODA=30”Į
=18£®
”ąOF=12£¬”ątan”ĻNOD=
=
=2£®
×÷”ĻNODµÄĘ½·ÖĻß½»NFÓŚµćG£¬¹żµćG×÷GH”ĶONÓŚµćH£¬ŌņFG=GH£®
”ąS
”÷ONF=
OF•NF=S
”÷OGF+S
”÷OGN=
OF•FG+
ON•GH=
£ØOF+ON£©•FG£®
”ąFG=
=
=
£¬
”ątan”ĻGOF=
=
=
£®
ÉčODÖŠ“¹ĻßÓėODµÄ½»µćĪŖK£¬ÓɶŌ³ĘŠŌæÉÖŖ£ŗ”ĻDPK=
”ĻDPO=
”ĻDON=”ĻFOG
”ątan”ĻDPK=
=
=
£¬
”ąPK=
£®
øł¾ŻĮāŠĪµÄ¶Ō³ĘŠŌæÉÖŖ£¬ŌŚĻ߶ĪODµÄĻĀ·½“ęŌŚÓėµćP¹ŲÓŚODÖį¶Ō³ĘµÄµćP”䣮
”ą“ęŌŚĮ½øöµćPµ½ODµÄ¾ąĄė¶¼ŹĒ
£®
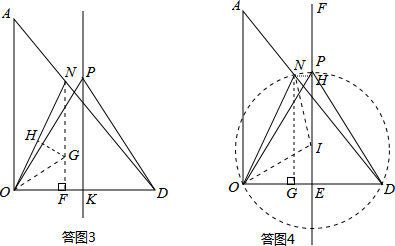
·½·Ø¶ž£ŗ“šĶ¼4ĖłŹ¾£¬×÷ONµÄ“¹Ö±Ę½·ÖĻߣ¬½»ODµÄ“¹Ö±Ę½·ÖĻßEFÓŚµćI£¬Į¬½įOI£¬IN£®
¹żµćN×÷NG”ĶOD£¬NH”ĶEF£¬“¹×ć·Ö±šĪŖG£¬H£®
µ±t=30Ź±£¬DN=OD=30£¬Ņ×ÖŖ”÷DNG”×”÷DAO£¬
”ą
==£¬¼“
==£®
”ąNG=24£¬DG=18£®
”ßEF“¹Ö±Ę½·ÖOD£¬
”ąOE=ED=15£¬EG=NH=3£®
ÉčOI=R£¬EI=x£¬Ōņ
ŌŚRt”÷OEIÖŠ£¬ÓŠR
2=15
2+x
2 ¢Ł
ŌŚRt”÷NIHÖŠ£¬ÓŠR
2=3
2+£Ø24-x£©
2 ¢Ś
ÓÉ¢Ł”¢¢ŚæÉµĆ£ŗ
”ąPE=PI+IE=
£®
øł¾Ż¶Ō³ĘŠŌæÉµĆ£¬ŌŚBDĻĀ·½»¹“ęŌŚŅ»øöµćP”äŅ²Āś×ćĢõ¼ž£®
”ą“ęŌŚĮ½øöµćP£¬µ½ODµÄ¾ąĄė¶¼ŹĒ
£®
£Ø×¢£ŗÖ»Ēó³öŅ»øöµćP²¢¼ĘĖćÕżČ·µÄæŪ£Ø1·Ö£©£®£©






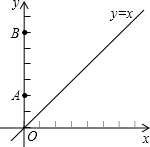 £Ø2013•ĮśŃŅ£©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬A£Ø0£¬2£©£¬B£Ø0£¬6£©£¬¶ÆµćCŌŚÖ±Ļßy=xÉĻ£®ČōŅŌA”¢B”¢CČżµćĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ£¬ŌņµćCµÄøöŹżŹĒ£Ø””””£©
£Ø2013•ĮśŃŅ£©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬A£Ø0£¬2£©£¬B£Ø0£¬6£©£¬¶ÆµćCŌŚÖ±Ļßy=xÉĻ£®ČōŅŌA”¢B”¢CČżµćĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ£¬ŌņµćCµÄøöŹżŹĒ£Ø””””£©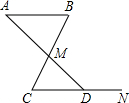 £Ø2013•ĮśŃŅ£©ČēĶ¼£¬AB”ĪCD£¬BCÓėADĻą½»ÓŚµćM£¬NŹĒÉäĻßCDÉĻµÄŅ»µć£®Čō”ĻB=65”ć£¬”ĻMDN=135”ć£¬Ōņ”ĻAMB=
£Ø2013•ĮśŃŅ£©ČēĶ¼£¬AB”ĪCD£¬BCÓėADĻą½»ÓŚµćM£¬NŹĒÉäĻßCDÉĻµÄŅ»µć£®Čō”ĻB=65”ć£¬”ĻMDN=135”ć£¬Ōņ”ĻAMB= £Ø2013•ĮśŃŅ£©ČēĶ¼£¬ĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪ£¬E”¢FŹĒ¶Ō½ĒĻßACÉĻµÄĮ½µć£¬”Ļ1=”Ļ2£®
£Ø2013•ĮśŃŅ£©ČēĶ¼£¬ĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪ£¬E”¢FŹĒ¶Ō½ĒĻßACÉĻµÄĮ½µć£¬”Ļ1=”Ļ2£®