
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
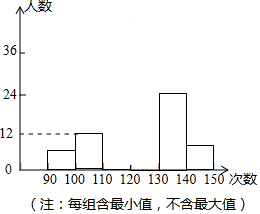 4月22日,垦利区九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频数和是18,乙同学计算出第一组的人数是抽取总人数的4%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
4月22日,垦利区九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频数和是18,乙同学计算出第一组的人数是抽取总人数的4%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
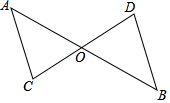 如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.
如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com