
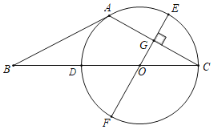
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,点O在BC上,⊙O经过点A,点C,且交BC于点D,直径EF⊥AC于点G.
(1)求证:AB是⊙O的切线;
(2)若AC=8,求BD的长.
【答案】(1)详见解析;(2)BD=![]() .
.
【解析】
(1)连接OA,由等腰三角形的性质得出∠B=∠C=30°,∠OAC=∠C=30°,求出∠OAB=120°﹣30°=90°,得出AB⊥OA,即可得出AB是⊙O的切线;
(2)由垂径定理得出AG=CG=![]() AC=4,由直角三角形的性质得出OG=
AC=4,由直角三角形的性质得出OG=![]() AG=
AG=![]() ,得出OA=2OG=
,得出OA=2OG=![]() ,BO=2OA=2OD,即可得出BD=OA=
,BO=2OA=2OD,即可得出BD=OA=![]() .
.
(1)如图,连接OA,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵OA=OC,
∴∠OAC=∠C=30°,
∴∠OAB=∠BAC-∠OAC=120°﹣30°=90°,
∴AB⊥OA,
∴AB是⊙O的切线.
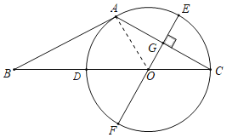
(2)解:∵直径EF⊥AC,
∴AG=CG=![]() AC=4,
AC=4,
∵∠OAC=30°,
∴OG=![]() AG=
AG=![]() ,
,
∴OA=2OG=![]() ,
,
∵∠OAB=90°,∠B=30°,
∴BO=2OA=2OD,
∴BD=OA=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
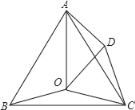
【题目】如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=2,OC=3,求AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,16,4分)如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .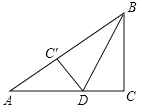
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A是△PBD的边BD上一点,以AB为直径的![]() 切PD于点C,过D作DE
切PD于点C,过D作DE![]() PO交PO延长线于点E,且有∠EDB=∠EPB.
PO交PO延长线于点E,且有∠EDB=∠EPB.
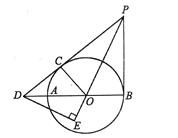
(1)求证:PB是圆O的切线.
(2)若PB=6,DB=8,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此变换进行下去,若点P(17,m)在这种连续变换的图象上,则m的值为( )
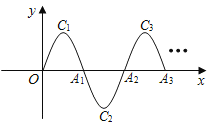
A.2B.﹣2C.﹣3D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店以每件80元的进价购进某种商品,原来按每件100元的售价出售,一天可售出50件;后经市场调查,发现这种商品每件的售价每降低2元,其销售量可增加10件.
(1)该网店销售该商品原来一天可获利润 元.
(2)设后来该商品每件售价降价![]() 元,网店一天可获利润
元,网店一天可获利润![]() 元.
元.
①若此网店为了尽可能增加该商品的销售量,且一天仍能获利1080元,则每件商品的售价应降价多少元?
②求![]() 与
与![]() 之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
查看答案和解析>>
科目:初中数学 来源: 题型:
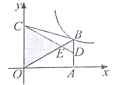
【题目】如图,四边形OABC中,AB∥OC,边OA在x轴的正半轴上,OC在y轴的正半轴上,点B在第一象限内,点D为AB的中点,CD与OB相交于点E,若△BDE、△OCE的面积分别为1和9,反比例函数y=![]() 的图象经过点B,则k=_______.
的图象经过点B,则k=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
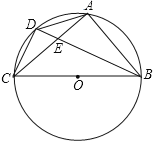
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧![]() 的中点BD交AC于点E.
的中点BD交AC于点E.
(1)求证:AD2=DEDB.
(2)若BC=5,CD=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com