已知:梯形两底分别为36cm和60cm,高为32cm,求这个梯形两腰延长后的交点到两底的距离.
【答案】
分析:过O作OF⊥BC于F,交AD于E,得出OE和OF的长是O到梯形ABCD的两底AD和BC上的距离,根据△OAD∽△OBC得出比例式,代入求出OE即可.
解答: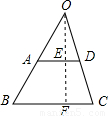
解:过O作OF⊥BC于F,交AD于E,
即OE和OF的长是O到梯形ABCD的两底AD和BC上的距离,
∵AD∥BC,
∴OE⊥AD,
∵AD∥BC,
∴△OAD∽△OBC,
∴
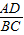
=
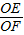
,
∵AD=36cm,BC=60cm,EF=32cm,
∴
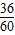
=
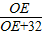
,
∴OE=48(cm),
∴OF=48cm+32cm=80cm,
答:这个梯形两腰延长后的交点到两底的距离分别是48cm,80cm.
点评:本题考查了梯形和相似三角形的性质和判定,注意:相似三角形的对应边之比等于对应边上的高之比.

 解:过O作OF⊥BC于F,交AD于E,
解:过O作OF⊥BC于F,交AD于E,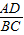 =
=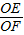 ,
,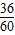 =
=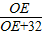 ,
,
